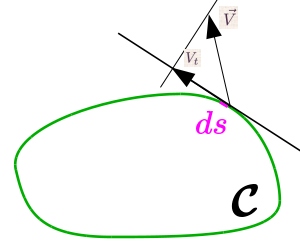
Circulation d'un champ de vecteurs
Dernière modif : 01/10/2016
La circulation d'un champ de vecteurs est liée au rotationnel du champ. Cette circulation va nous être utile pour démontrer que l'électromagnétisme est une théorie relativiste.
[ lien vers L'article.pdf ]
articles précédent et suivant dans la série :
Rotationnel d'un champ de vecteurs
Les Equations de Maxwell


Ci-dessous le premier article de la série ANALYSE (complexe, harmonique):
Les nombres complexes


Ci-dessous le premier article de la série CALCUL VECTORIEL :
CALCUL VECTORIEL



Liens...
Remarque : J'ai rédigé cet article en Latex avec TexMacs sous Linux Min18 (TexMacs ne tourne pas sous Mint19 !!!)). Ensuite, afin de pouvoir l'afficher sur cette page html calculée en php, je l'ai exporté sous forme d'un document au format pdf.
6258
[ Retour Accueil ]
Ce site est développé en PHP avec des LOGICIELS LIBRES sous LINUX