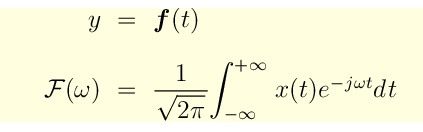Transformée de Fourier sur ATmega32 et Arduino Mega2560
La rapidité d'exécution du calcul est essentielle lorsqu'il s'agit de traiter
un signal en temps réel. Elle déterminera la fréquence maximale qui puisse
être analysée.
1 La partie théorique
Je vous invite dans un premier temps, si ce n'est déjà fait, à consulter l'étude analytique de la Transformée de Fourier Rapide sur mes pages pleines de jolies équations mathématiques commentées :
|
 |
|
|
2 Le programme en C++ et Qt4
|
|
|
La page principale :
CODE SOURCE C++ Qt4
/* Programme écrit par Silicium628 ce logiciel est libre et open source */ #include "mainwindow.h" #include "ui_mainwindow.h" #include "math.h" #include "complexe.cpp" QString version = "2.4"; QColor couleur_ecran = QColor::fromRgb(3, 41, 11, 255); QColor couleur_ligne = QColor::fromRgb(167, 2, 0, 255); QColor couleur_trace = QColor::fromRgb(0, 210, 0, 255); QColor couleur_texte = QColor::fromRgb(255, 255, 0, 255); QColor couleur_signature = QColor::fromRgb(255, 255, 0, 255); QPen pen_ligne(couleur_ligne, 1, Qt::SolidLine); QPen pen_trace(couleur_trace, 1, Qt::SolidLine); QPen pen_reticule(couleur_ligne, 1, Qt::SolidLine); Complexe ech[1024]; // nb_ech echantillons Complexe tab_X[1024]; // nb_ech valeurs traitées Complexe tab_W[512]; // nb_ech/2 float frequence1=400; // Hz float frequence2=400; // Hz float frequence3=100; // Hz uint nb_etapes=8; uint nb_ech = pow (2,nb_etapes); // nombre d'échantillons = 2 puissance(nb_etapes) float frq_echantillonnage=16*frequence1; // Hz float Te; // période d'échantillonage //int pas_balayage=40; int hamming = false; int second_Frq = false; int bz = false; int modul = false; MainWindow::MainWindow(QWidget *parent) : QMainWindow(parent) { setupUi(this); setWindowTitle("Transformee de Fourier Rapide FFT - version " + version); scene = new QGraphicsScene(this); scene->setBackgroundBrush(couleur_ecran); graphicsView1->setScene(scene); graphicsView1->setGeometry(0,0,530,430); groupe_reticule = new QGraphicsItemGroup(); scene->addItem(groupe_reticule); groupe_trace = new QGraphicsItemGroup(); scene->addItem(groupe_trace); calcul_tableau_W(); tracer_graduations(); } void MainWindow::effacer_graduation() { foreach( QGraphicsItem *item, scene->items( groupe_reticule->boundingRect() ) ) { if( item->group() == groupe_reticule ) { delete item; } } } void MainWindow::effacer_trace() { foreach( QGraphicsItem *item, scene->items( groupe_trace->boundingRect() ) ) { if( item->group() == groupe_trace ) { delete item; } } } MainWindow::~MainWindow() { } void MainWindow::tracer_graduations() { float i,x,y; float nb_grad_max; float intervalle; // séparant les graduations float fi; QString sti; uint decal = 3; // leger decallage vertical pour ne pas masquer la trace rectangle = new QGraphicsRectItem(0,decal, 511, 400); rectangle->setPen(couleur_ligne); groupe_trace->addToGroup(rectangle); // lignes verticales // ici calcul de l'intervalle (en pixels) qui correspond exactement à 100Hz (en fréquence) intervalle = 2000.0 * nb_ech * 2.0 / (frq_echantillonnage); nb_grad_max = 512 / intervalle; for (i=0; i<=nb_grad_max; i++) { x = intervalle * i; ligne1 = new QGraphicsLineItem(x, decal, x, 400 + decal); ligne1->setPen(pen_reticule); groupe_reticule->addToGroup(ligne1); fi = x * frq_echantillonnage / nb_ech /4; sti.setNum(fi); texte_frq = new QGraphicsTextItem(sti); texte_frq->setDefaultTextColor(couleur_texte); texte_frq->setPos(x,380); if(x<480) // évite que l'écriture ne déborde du cadre a droite { groupe_reticule->addToGroup(texte_frq); } } // lignes horizontales intervalle = 50; nb_grad_max = 400 / intervalle; for (i=0; i<=nb_grad_max; i++) { y = 400 + decal - intervalle * i; ligne1 = new QGraphicsLineItem(0, y, 511, y); ligne1->setPen(pen_reticule); groupe_reticule->addToGroup(ligne1); } texte_frq = new QGraphicsTextItem("Silicium628"); texte_frq->setDefaultTextColor(couleur_signature); texte_frq->setPos(5,5); groupe_reticule->addToGroup(texte_frq); scene->addItem(groupe_reticule); } void MainWindow::tracer_signal() { uint offset_y = 100; float echelle =1024/nb_ech; uint n; float x, y, memo_x, memo_y; segment_trace = new QGraphicsLineItem(0, offset_y, 512, offset_y); segment_trace->setPen(couleur_ligne); groupe_trace->addToGroup(segment_trace); effacer_trace(); x=0; y=offset_y; for(n=0; n<nb_ech; n++) { memo_x = x; memo_y = y; x = echelle * n /2; y = offset_y - 20 * ech[n].a; segment_trace = new QGraphicsLineItem(memo_x ,memo_y, x, y); segment_trace->setPen(pen_trace); groupe_trace->addToGroup(segment_trace); } scene->addItem(groupe_trace); } void MainWindow::tracer_tableau_valeurs() { uint offset_y = 350; // 600 float echelle =1024/nb_ech; uint n; float x, y, memo_x, memo_y; int z; if (bz) {z=4;} else {z=1;} segment_trace = new QGraphicsLineItem(0, offset_y, 512, offset_y); segment_trace->setPen(couleur_ligne); groupe_trace->addToGroup(segment_trace); x=0; y=offset_y; for(n=0; n<nb_ech/2; n++) { memo_x = x; memo_y = y; x = echelle * n; y = offset_y - z * sqrt( tab_X[n].a * tab_X[n].a + tab_X[n].b * tab_X[n].b ); segment_trace = new QGraphicsLineItem(memo_x ,memo_y, x, y); segment_trace->setPen(pen_trace); groupe_trace->addToGroup(segment_trace); } scene->addItem(groupe_trace); } void MainWindow::RAZ_tableau_echantillons() { uint n; for(n=0; n < nb_ech; n++) { ech[n].a = 0; // partie reelle ech[n].b = 0; // partie imaginaire } } void MainWindow::remplir_tableau_echantillons() { // création du signal à analyser uint n, n_max; float x; Te = 1.0 / frq_echantillonnage; if (bz==true) {n_max = nb_ech /4; } else {n_max = nb_ech; } for(n=0; n < n_max; n++) // nb d'échantillons { x= cos(2.0 * M_PI * frequence1 * n * Te ); if (modul) {x *= 1 + 0.8 * cos(2 * M_PI * frequence3 * n * Te);} // modulation d'amplitude if (second_Frq) {x+=cos(2 * M_PI * frequence2 * n * Te); } if (hamming) { x = x * (1- cos (2* M_PI * n / n_max ));} ech[n].a = x; // partie reelle ech[n].b = 0; // partie imaginaire } } //void MainWindow::remplir_tableau_echantillons() //{ //// création du signal à analyser // uint n; // float x; // Te = 1.0 / frq_echantillonnage; // for(n=0; n < nb_ech; n++) // nb d'échantillons // { // if ((n >= 50) and (n<=55)) {ech[n].a = 30;} else {ech[n].a = 0;} // } //} uint bit_reversal(uint num, uint nb_bits) { uint r = 0, i, s; if ( num > (1<< nb_bits)) { return 0; } for (i=0; i<nb_bits; i++) { s = (num & (1 << i)); if(s) { r |= (1 << ((nb_bits - 1) - i)); } } return r; } void MainWindow::bit_reverse_tableau_X() { // recopie les échantillons en les classant dans l'ordre 'bit reverse' uint n,r; for(n=0; n < nb_ech; n++) // nb d'échantillons { r=bit_reversal(n,nb_etapes); tab_X[n] = ech[r]; } } void MainWindow::calcul_tableau_W() { // calcul et memorisation dans un tableau des twiddle factors uint n; float x; for(n=0; n<(nb_ech/2-1); n++) { x=2.0*M_PI * n / nb_ech; tab_W[n].a = cos(x); // partie reelle tab_W[n].b = -sin(x); // partie imaginaire } } void MainWindow::calcul_fourier() { Complexe produit; // voir la classe "Complexe" : complexe.h et complexe.ccp uint etape, e1, e2, li, w, ci; uint li_max=nb_ech; e2=1; for (etape=1; etape<=nb_etapes; etape++) { e1=e2; //(e1 evite d'effectuer des divisions e2/2 plus bas) e2=e2+e2; for (li=0; li<li_max; li+=1) { ci=li & (e2-1); // ET bit à bit if (ci>(e1-1)) { w=li_max/e2*(li & (e1 -1)); // ET bit à bit calcul du numéro du facteur de tripatouillages W produit = tab_W[w] * tab_X[li]; // le twiddle factor est lu en memoire; le produit est une mutiplication de nb complexes. Voir "complexe.cpp" tab_X[li]=tab_X[li-e1]-produit; // concerne la ligne basse du croisillon; soustraction complexe; Voir "complexe.cpp" tab_X[li-e1]=tab_X[li-e1] + produit; // concerne la ligne haute du croisillon; addition complexe; Voir "complexe.cpp" } } } } void MainWindow::on_btn2_clicked() // BOUTON "FOURIER" { effacer_trace(); calcul_tableau_W(); RAZ_tableau_echantillons(); remplir_tableau_echantillons(); tracer_signal(); bit_reverse_tableau_X(); calcul_fourier(); tracer_graduations(); tracer_tableau_valeurs(); } void MainWindow::on_spinBox_frq_valueChanged(int arg1) // SELECTEUR DE FREQUENCE 1 { effacer_trace(); frequence1 = arg1; RAZ_tableau_echantillons(); remplir_tableau_echantillons(); tracer_signal(); calcul_tableau_W(); bit_reverse_tableau_X(); calcul_fourier(); // tracer_graduations(); tracer_tableau_valeurs(); } void MainWindow::on_spinBox_frq_2_valueChanged(int arg1) // SELECTEUR DE FREQUENCE 2 { effacer_trace(); frequence2 = arg1; RAZ_tableau_echantillons(); remplir_tableau_echantillons(); tracer_signal(); calcul_tableau_W(); bit_reverse_tableau_X(); calcul_fourier(); // tracer_graduations(); tracer_tableau_valeurs(); } void MainWindow::on_spinBox_frq_3_valueChanged(int arg1) { effacer_trace(); frequence3 = arg1; RAZ_tableau_echantillons(); remplir_tableau_echantillons(); tracer_signal(); calcul_tableau_W(); bit_reverse_tableau_X(); calcul_fourier(); // tracer_graduations(); tracer_tableau_valeurs(); } void MainWindow::on_checkBox1_toggled(bool checked) // HAMMING { effacer_trace(); if (checked) {hamming = true;} else {hamming = false;} RAZ_tableau_echantillons(); remplir_tableau_echantillons(); tracer_signal(); calcul_tableau_W(); bit_reverse_tableau_X(); calcul_fourier(); // tracer_graduations(); tracer_tableau_valeurs(); } void MainWindow::on_checkBox2_toggled(bool checked) // SECONDE FREQUENCE { effacer_trace(); if (checked) {second_Frq = true;} else {second_Frq = false;} RAZ_tableau_echantillons(); remplir_tableau_echantillons(); tracer_signal(); calcul_tableau_W(); bit_reverse_tableau_X(); calcul_fourier(); // tracer_graduations(); tracer_tableau_valeurs(); } void MainWindow::on_checkBox3_toggled(bool checked) { effacer_trace(); if (checked) {bz = true;} else {bz = false;} RAZ_tableau_echantillons(); remplir_tableau_echantillons(); tracer_signal(); calcul_tableau_W(); bit_reverse_tableau_X(); calcul_fourier(); // tracer_graduations(); tracer_tableau_valeurs(); } void MainWindow::on_checkBox4_clicked(bool checked) { effacer_trace(); if (checked) {modul = true;} else {modul = false;} RAZ_tableau_echantillons(); remplir_tableau_echantillons(); tracer_signal(); calcul_tableau_W(); bit_reverse_tableau_X(); calcul_fourier(); // tracer_graduations(); tracer_tableau_valeurs(); }
|
3 -
Le code de la classe "Complexe" : complexe.ccp
|
|
|
|
5 Saisie d'écran de l'exécutable :
|
Le tracé du haut représente le signal temporel tel qu'il est échantillonné. Celui du bas représente sa transformée de Fourier (spectre fréquentiel). Bien que le nombre de points soit identique dans les deux cas (512 points), les unités ne sont pas les mêmes, des millisecondes en haut et des Hertz en bas.
Les courbes sont mises à jour automatiquement ("instantanément" dirons nous, vu la puissance de nos ordinateurs) lorsqu'on modifie les fréquences à la souris.
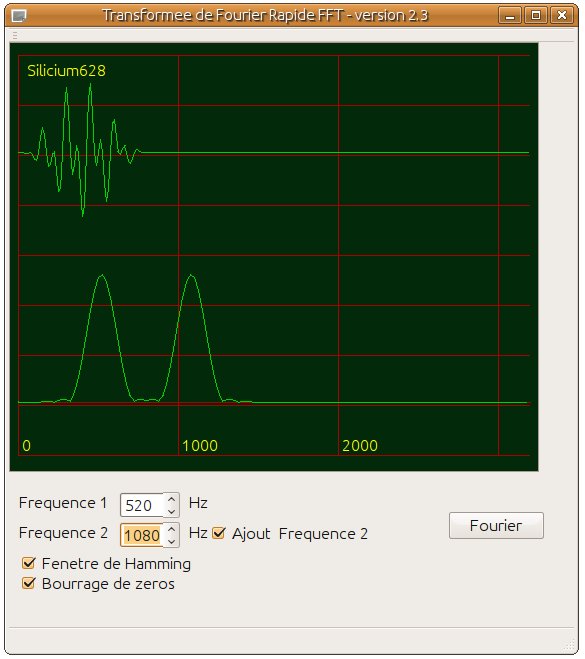
Le programme peut calculer la transformée de la somme de deux signaux sinusoïdaux de fréquences différentes.
La technique de "bourrage de zéros" (dont je n'ai pas parlé) est prise en compte. Utilisée conjointement avec la fenêtre de Hamming pour un signal constitué de deux sinusoïdes, elle permet d'obtenir des effets "remarquables" lorsque les deux fréquences se rapprochent puis se croisent... Je vous laisse découvrir cela.
Des modifications simples de ce programme peuvent permettre d’analyser d'autres formes d'ondes.
|
 |
|
|
7 Version en C (n'utilisant pas la class 'complexes')
|
Il m'a été demandé s'il était possible de programmer la FFT en langage C plutôt qu'en C++, en particulier sans faire appel à la class (objet) 'Complexe'. ça tombe bien, cela faisait partie de mes projets afin de pouvoir à terme implémenter la FFT sur un microcontrôleur ATmega.
Voici donc le code dans lequel j'ai remplacé les manipulations de l'objet appelé 'complexe' par des opérations arithmétiques classiques sur les parties réelles et imaginaires et les tableaux de nombres complexes par des tableaux de deux nombres réels (partie réelle et imaginaire).
Le code obtenu est moins élégant, il perd en lisibilité, mais il constitue le premier pas vers la portabilité sur ATmega que je publierai prochainement.
Ce qui reste du code en C++ et Qt4 ne concerne que l'affichage sur PC, sur l'ATmega ce sera remplacé par quelques opérations de lecture-écriture sur fichiers ou acquisition directe en entrée et sortie sur affichage (Module LCD 84*48 Nokia 5110 par exemple)
|
 |
|
|
8 -
Le programme en C (sans la class 'Complexe') :
CODE SOURCE C++ Qt4
/* Programme écrit par Silicium628 ce logiciel est libre et open source 12 juin 2014 cette version dérive du projet "FTT" Il a pour but de tester la faisabilité de programmer la transformée en C et non en C++, c'est à dire sans faire appel à la programmation orientée objet. afin de l'implémenter sur un uC ATmega8 */ #include "mainwindow.h" #include "ui_mainwindow.h" #include "math.h" QString version = "2.0"; QColor couleur_ecran = QColor::fromRgb(3, 41, 11, 255); QColor couleur_ligne = QColor::fromRgb(167, 2, 0, 255); QColor couleur_trace = QColor::fromRgb(0, 210, 0, 255); QColor couleur_texte = QColor::fromRgb(255, 255, 0, 255); QColor couleur_signature = QColor::fromRgb(255, 255, 0, 255); QPen pen_ligne(couleur_ligne, 1, Qt::SolidLine); QPen pen_trace(couleur_trace, 1, Qt::SolidLine); QPen pen_reticule(couleur_ligne, 1, Qt::SolidLine); typedef float complexe[2]; //complexe ech[84]; // nb_ech echantillons 1024 SUPPRIME ! et oui !! j'utilise le même tableau pour tout ! complexe tab_X[84]; // nb_ech valeurs traitées 1024 complexe tab_W[42]; // nb_ech/2 512 float frequence1=400; // Hz float frequence2=400; // Hz uint nb_etapes=6; //8 uint nb_ech = pow (2,nb_etapes); // nombre d'échantillons = 2 puissance(nb_etapes) float frq_echantillonnage=8*frequence1; // Hz float Te; // période d'échantillonage //int pas_balayage=40; int hamming = true; int second_Frq = false; int bz = true; uint forme; MainWindow::MainWindow(QWidget *parent) : QMainWindow(parent) { setupUi(this); setWindowTitle("Transformee de Fourier Rapide FFT (no objects) - version " + version); scene = new QGraphicsScene(this); // scene->setBackgroundBrush(couleur_ecran); graphicsView1->setScene(scene); // graphicsView1->setGeometry(0,0,530,430); graphicsView1->setGeometry(140,30,84,48); groupe_reticule = new QGraphicsItemGroup(); scene->addItem(groupe_reticule); groupe_trace = new QGraphicsItemGroup(); scene->addItem(groupe_trace); effacer_trace(); RAZ_tableau_echantillons(); remplir_tableau_echantillons(); // tracer_signal(); calcul_tableau_W(); // bit_reverse_tableau_X(); calcul_fourier(); tracer_tableau_valeurs(); } void MainWindow::effacer_graduation() { foreach( QGraphicsItem *item, scene->items( groupe_reticule->boundingRect() ) ) { if( item->group() == groupe_reticule ) { delete item; } } } void MainWindow::effacer_trace() { foreach( QGraphicsItem *item, scene->items( groupe_trace->boundingRect() ) ) { if( item->group() == groupe_trace ) { delete item; } } } MainWindow::~MainWindow() { } void MainWindow::tracer_graduations() { float i,x,y; float nb_grad_max; float intervalle; // séparant les graduations float fi; QString sti; uint decal = 3; // leger decallage vertical pour ne pas masquer la trace rectangle = new QGraphicsRectItem(0,decal, 511, 400); rectangle->setPen(couleur_ligne); groupe_trace->addToGroup(rectangle); // lignes verticales // ici calcul de l'intervalle (en pixels) qui correspond exactement à 100Hz (en fréquence) intervalle = 2000.0 * nb_ech * 2.0 / (frq_echantillonnage); nb_grad_max = 512 / intervalle; for (i=0; i<=nb_grad_max; i++) { x = intervalle * i; ligne1 = new QGraphicsLineItem(x, decal, x, 400 + decal); ligne1->setPen(pen_reticule); groupe_reticule->addToGroup(ligne1); fi = x * frq_echantillonnage / nb_ech /4; sti.setNum(fi); texte_frq = new QGraphicsTextItem(sti); texte_frq->setDefaultTextColor(couleur_texte); texte_frq->setPos(x,380); if(x<480) // évite que l'écriture ne déborde du cadre a droite { groupe_reticule->addToGroup(texte_frq); } } // lignes horizontales intervalle = 50; nb_grad_max = 400 / intervalle; for (i=0; i<=nb_grad_max; i++) { y = 400 + decal - intervalle * i; ligne1 = new QGraphicsLineItem(0, y, 511, y); ligne1->setPen(pen_reticule); groupe_reticule->addToGroup(ligne1); } texte_frq = new QGraphicsTextItem("Silicium628"); texte_frq->setDefaultTextColor(couleur_signature); texte_frq->setPos(5,5); groupe_reticule->addToGroup(texte_frq); scene->addItem(groupe_reticule); } void MainWindow::tracer_signal() { uint offset_y = 24; float echelle =168/nb_ech; uint n; float x, y, memo_x, memo_y; segment_trace = new QGraphicsLineItem(0, offset_y, 512, offset_y); segment_trace->setPen(couleur_ligne); groupe_trace->addToGroup(segment_trace); effacer_trace(); x=0; y=offset_y; for(n=0; n<64; n++) { memo_x = x; memo_y = y; x = n; y = offset_y - 10 * tab_X[n][1]; // partie réelle segment_trace = new QGraphicsLineItem(memo_x ,memo_y, x, y); segment_trace->setPen(pen_trace); groupe_trace->addToGroup(segment_trace); } scene->addItem(groupe_trace); } void MainWindow::tracer_tableau_valeurs() { uint offset_y = 46; // 600 float echelle =168/nb_ech; uint n; float x, y, memo_x, memo_y; int z; if (bz) {z=4;} else {z=1;} segment_trace = new QGraphicsLineItem(0, offset_y, 84, offset_y); segment_trace->setPen(couleur_ligne); groupe_trace->addToGroup(segment_trace); x=0; y=offset_y; for(n=0; n<nb_ech/2; n++) { memo_x = x; memo_y = y; x = echelle * n; // y = offset_y - z * sqrt( tab_X[n][1] * tab_X[n][1] + tab_X[n][2] * tab_X[n][2] ); // a=parties réelles, b=parties imaginaires //version sans la racine carrée sqrt (qui pose des problèmes sur ATmega avr-gcc): y = offset_y - z * ( tab_X[n][1] * tab_X[n][1] + tab_X[n][2] * tab_X[n][2] ) / 8; // a=parties réelles, b=parties imaginaires segment_trace = new QGraphicsLineItem(memo_x ,memo_y, x, y); segment_trace->setPen(pen_trace); groupe_trace->addToGroup(segment_trace); } scene->addItem(groupe_trace); } void MainWindow::RAZ_tableau_echantillons() { uint n; for(n=0; n < nb_ech; n++) { tab_X[n][1] = 0; // partie reelle tab_X[n][2] = 0; // partie imaginaire } } uint bit_reversal(uint num, uint nb_bits) { uint r = 0, i, s; if ( num > 1<< nb_bits) { return 0; } for (i=0; i<nb_bits; i++) { s = (num & (1 << i)); if(s) { r |= (1 << ((nb_bits - 1) - i)); } } return r; } void MainWindow::remplir_tableau_echantillons() { // création du signal à analyser uint n, r, n_max; float x; Te = 1.0 / frq_echantillonnage; if (bz==true) {n_max = nb_ech /4; } else {n_max = nb_ech; } for(n=0; n < n_max; n++) // nb d'échantillons { x= cos(2.0 * M_PI * frequence1 * n * Te ); if (second_Frq) {x+=cos(2 * M_PI * frequence2 * n * Te); } if (hamming) { x = x * (1- cos (2* M_PI * n / n_max ));} r=bit_reversal(n,nb_etapes); tab_X[r][1] = x; // partie reelle tab_X[r][2] = 0; // partie imaginaire } } /* void MainWindow::bit_reverse_tableau_X() { // recopie les échantillons en les classant dans l'ordre 'bit reverse' uint n,r; for(n=0; n < nb_ech; n++) // nb d'échantillons { r=bit_reversal(n,nb_etapes); tab_X[n][1] = ech[r][1]; tab_X[n][2] = ech[r][2]; } } */ void MainWindow::calcul_tableau_W() { // calcul et memorisation dans un tableau des twiddle factors uint n; float x; for(n=0; n<(nb_ech/2-1); n++) { x=2.0*M_PI * n / nb_ech; tab_W[n][1] = cos(x); // partie reelle tab_W[n][2] = -sin(x); // partie imaginaire } } void MainWindow::calcul_fourier() { complexe produit; // voir le type "complexe" déclaré plus haut uint decal =2; uint etape, e1, e2, li, w, ci; uint li_max=nb_ech; e2=1; for (etape=1; etape<=nb_etapes; etape++) { e1=e2; //(e1 evite d'effectuer des divisions e2/2 plus bas) e2=e2+e2; for (li=0; li<li_max; li+=1) { ci=li & (e2-1); // ET bit à bit if (ci>(e1-1)) { w=li_max/e2*(li & (e1 -1)); // ET bit à bit calcul du numéro du facteur de tripatouillages W produit[1]=tab_W[w][1]*tab_X[li][1]-tab_W[w][2]*tab_X[li][2]; produit[2]=tab_W[w][1]*tab_X[li][2]+tab_W[w][2]*tab_X[li][1]; tab_X[li][1]=tab_X[li-e1][1]-produit[1]; tab_X[li][2]=tab_X[li-e1][2]-produit[2]; tab_X[li-e1][1]=tab_X[li-e1][1]+produit[1]; tab_X[li-e1][2]=tab_X[li-e1][2]+produit[2]; } } } } void MainWindow::on_spinBox_frq_valueChanged(int arg1) // SELECTEUR DE FREQUENCE 1 { effacer_trace(); frequence1 = arg1; RAZ_tableau_echantillons(); remplir_tableau_echantillons(); // tracer_signal(); calcul_tableau_W(); // bit_reverse_tableau_X(); calcul_fourier(); tracer_tableau_valeurs(); } void MainWindow::on_spinBox_frq_2_valueChanged(int arg1) // SELECTEUR DE FREQUENCE 2 { effacer_trace(); frequence2 = arg1; RAZ_tableau_echantillons(); remplir_tableau_echantillons(); // tracer_signal(); calcul_tableau_W(); // bit_reverse_tableau_X(); calcul_fourier(); tracer_tableau_valeurs(); } void MainWindow::on_checkBox1_toggled(bool checked) // HAMMING { effacer_trace(); if (checked) {hamming = true;} else {hamming = false;} RAZ_tableau_echantillons(); remplir_tableau_echantillons(); // tracer_signal(); calcul_tableau_W(); // bit_reverse_tableau_X(); calcul_fourier(); tracer_tableau_valeurs(); } void MainWindow::on_checkBox2_toggled(bool checked) // SECONDE FREQUENCE { effacer_trace(); if (checked) {second_Frq = true;} else {second_Frq = false;} RAZ_tableau_echantillons(); remplir_tableau_echantillons(); // tracer_signal(); calcul_tableau_W(); // bit_reverse_tableau_X(); calcul_fourier(); tracer_tableau_valeurs(); } void MainWindow::on_checkBox3_toggled(bool checked) { effacer_trace(); if (checked) {bz = true;} else {bz = false;} RAZ_tableau_echantillons(); remplir_tableau_echantillons(); // tracer_signal(); calcul_tableau_W(); // bit_reverse_tableau_X(); calcul_fourier(); tracer_tableau_valeurs(); }
|
|
|
|
9 -
|
21 juin 2014:
Je viens de supprimer le tableau des valeurs d'entrées, j'utilise directement le tableau de travail. (84x2x4 = 672 octets de gagnés en RAM une fois le programme implémenté sur un ATmega. C'est l'ATmega32 (2k SRAM) qui va être content !!! Sans ça j'aurais dû utiliser un ATmega128 (8k RAM) parce que j'ai besoin de pas mal de RAM également pour gérer efficacement l'afficheur LCD Nokia 5110.
A ce propos je vous signale que j'ai fini (hier) cette implémentation sur ATmega et que ça fonctionne parfaitement. Il me reste plus qu'à entrer les valeurs avec le convertisseur A/N, à toiletter un peu le source obtenu et à la publier ici, ce qui ne devrait pas tarder, promis !
|
J'ai supprimé une vidéo ici parce que Dailymotion m'y incrustait une pub au début. Ce site n'est pas un panneau publicitaire !
|
|
|
10 Implémentation de la Transformée de Fourier Rapide sur ATmega32
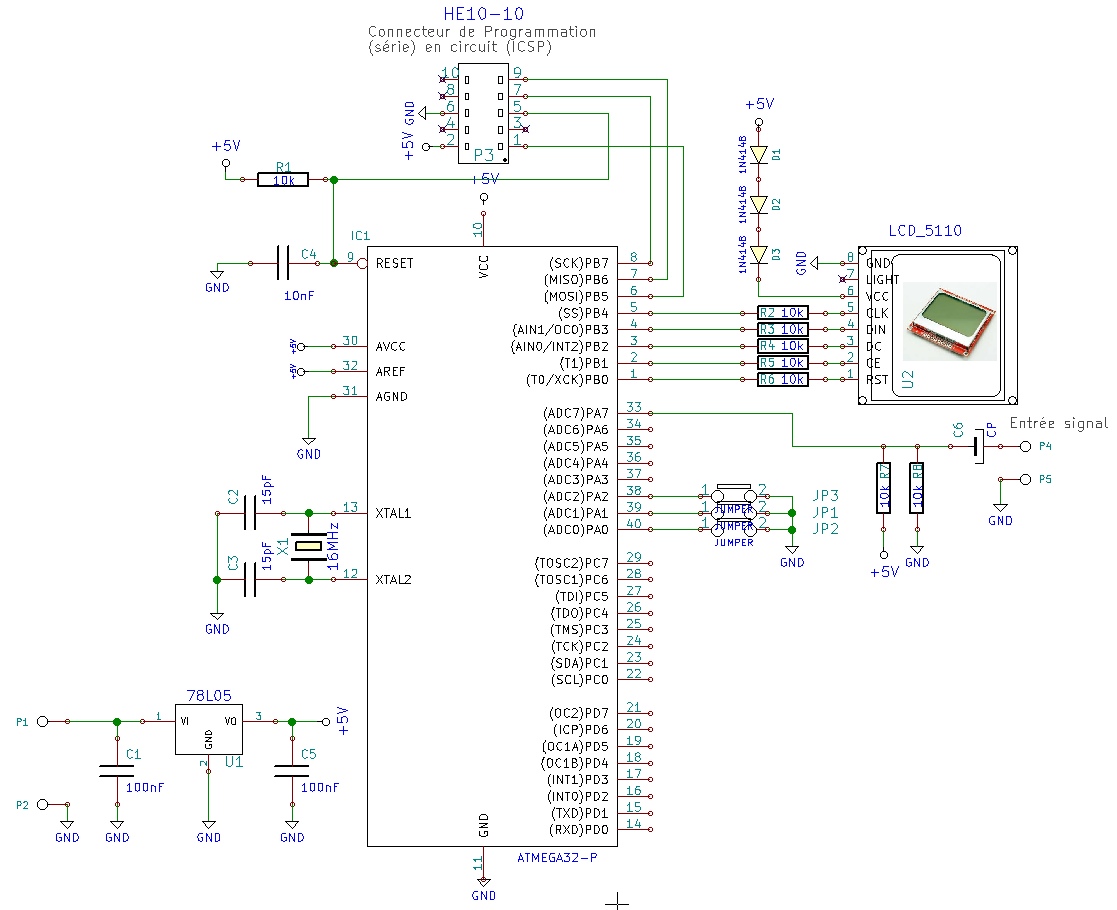 |
|
|
|
11 -
|
Le premier jump permet de choisir entre visualiser le signal d'entrée ou bien sa transformée de Fourier.
Le deux suivants permettent d'appliquer (ou non) le hamming et le bourrage de zéros.
Le signal d'entrée doit avoir une amplitude de 1V environ et une fréquence comprise entre 100 Hz et 700 Hz.
Je vais pouvoir augmenter cette fréquence par simple changement des paramètres du CONV A/N de l'ATmega. A suivre donc...
|
|
|
|
12 -
|
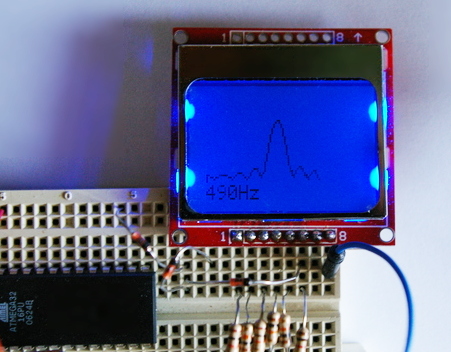
22 juin 2014:
Nouvel affichage avec une courbe fine en place des bâtons verticaux;
La courbe est obtenue pour le calcul avec une fenêtre d'acquisition rectangulaire (au lieu de la fenêtre de hamming utilisée précédemment pour la vidéo). On distingue nettement les lobes secondaires de part et d'autre du pic central, malgré la (très) faible résolution de l'afficheur Nokia 5110 (84x48 pixels).
C'est une expérience qui repose sur une démonstration mathématique relativement corsée mais qui reste réalisable par tout un chacun pour une somme modique, de l'ordre de 5 euro en commandant l'ATmega et le LCD sur eBay. (Je me permets de donner ce mauvais conseil parce qu'il est difficile de trouver des ATmega32 chez l'épicier du coin).
|
 |
|
|
13 Le programme (firmware) en C pour l'ATmega
CODE SOURCE pour ATmega32
/*************************** FFT.cpp par Silicium628 logiciel Libre Open Source ****************************/ #include <avr/io.h> #include <stdint.h> #include <stdlib.h> #include "timeout.h" // comprend : #define F_CPU 16000000UL // 16 MHz #include "LCD_5110.cpp" #include <math.h> const char *version = "2.5"; // ( signal entrant 10kHz à 90kHz ) typedef float complexe[2]; complexe tab_X[64]; // nb_ech valeurs traitées complexe tab_W[32]; // nb_ech/2 float frequence1; // Hz float frq_echantillonnage; // Hz const uint8_t nb_etapes=6; uint8_t nb_ech = pow (2,nb_etapes); // nombre d'échantillons = 2 puissance(nb_etapes) char hamming; char bourrage; char mode_affi; //const uint8_t hamming = false; //const uint8_t bourrage = true; void RAZ_tableau_echantillons() { uint8_t n; for(n=0; n < nb_ech; n++) { tab_X[n][1] = 0; // partie reelle tab_X[n][2] = 0; // partie imaginaire } } void init_ports (void) // ports perso // 0 = entree, 1=sortie ; les 1 sur les pins en entrees activent les R de Pull Up (tirage à VCC) { PORTA = 0b00000111; DDRA = 0b01111000; //PA7 en entree (ADC7 - entrée signal); PA0, PA1, PA2 jumpers à GND. PORTB = 0b00000000; DDRB |= 0b11111111; PORTC = 0b00000000; DDRC = 0b11111111; PORTD = 0b00000000; DDRD = 0b11111111; } /* The ADC module contains a prescaler, which generates an acceptable ADC clock fre- quency from any CPU frequency above 100 kHz. The prescaling is set by the ADPS bits in ADCSRA */ void InitADC (void) { // SFIOR = 0b10000000; // ADTS2,1,0 = 100 -> CAN declenché par Timer0 Overflow - p:218 ADMUX = 0b01000111; //Bit 7:6 = ADC Reference Selection = 01 -> AVCC ; //Bits 0:4 - Analog Channel Selection Bits et gain éventuel - p214 // ici Select pin ADC7 using MUX avec ref tension interne = AREF externe - pas de gain. /** CHOISIR UNE SEULE LIGNE CI-DESSOUS pour ADCSRA */ // parametrage gamme 8-90 kHz ADCSRA = 0b10000010; // bit7: Activate ADC; ADPS2..0->Prescaler=f/4 ; bit5 = ADATE (ADC Auto Trigger Enable)->non utilisé ici - p:216 et 218 // parametrage gamme 4-56 kHz // ADCSRA = 0b10000011; // bit7: Activate ADC; ADPS2..0->Prescaler=f/8 ; bit5 = ADATE (ADC Auto Trigger Enable)->non utilisé ici - p:216 et 218 // parametrage gamme 2-31 kHz // ADCSRA = 0b10000100; // bit7: Activate ADC; ADPS2..0->Prescaler=f/16 ; bit5 = ADATE (ADC Auto Trigger Enable)->non utilisé ici - p:216 et 218 // parametrage gamme 1-15 kHz // ADCSRA = 0b10000101; // bit7: Activate ADC; ADPS2..0->Prescaler=f/32 ; bit5 = ADATE (ADC Auto Trigger Enable)->non utilisé ici - p:216 et 218 // parametrage gamme 300 Hz-8000 Hz // ADCSRA = 0b10000110; // bit7: Activate ADC; ADPS2..0->Prescaler=f/32 ; bit5 = ADATE (ADC Auto Trigger Enable)->non utilisé ici - p:216 et 218 // parametrage gamme 200 Hz- 4300 Hz // ADCSRA = 0b10000111; // bit7: Activate ADC; ADPS2..0->Prescaler=f/32 ; bit5 = ADATE (ADC Auto Trigger Enable)->non utilisé ici - p:216 et 218 } uint8_t bit_reversal(uint8_t num, uint8_t nb_bits) { uint8_t r = 0, i, s; if ( num > 1<< nb_bits) { return 0; } for (i=0; i<nb_bits; i++) { s = (num & (1 << i)); if(s) { r |= (1 << ((nb_bits - 1) - i)); } } return r; } /*********************************************************************** Remarques : - si l'on veut augmenter la vitesse d'acquisition et maîtriser précisément sa durée d'exécution il y a lieu de remplacer la fonction "acquisition()" par une routine écrite en assembleur et faire appel à une interruption pour le timing. - si l'on veut de plus augmenter la vitesse du traitement de la FFT, il faudra remplacer la fonction "calcul_fourier()" par une routine en assembleur, et en fait dans ce cas on envisagera de réécrire tout le programme en assembleur. - si on désire une plus grande rapidité encore, on pourra se tourner vers un microcontrôleur ARM cadencé à... 700 MHz (voire plus) et on pense alors bien sûr au Raspberry Pi ! - si l'on veut calculer encore plus vite on peut utiliser le processeur d'une carte graphique, (par exemple en 2014 une Nvidia GeForce GTX680 dont le processeur tourne à à 2GHz- 2Go - DDR5 ou une Nvidia Quadro 6000 ) ou au moins le FPU intégré dans les microprocesseurs de nos ordinateurs. - et si... on exige encore plus de vitesse on se tournera vers un Field Programmable Gate Arrays (FPGA) ou processeur de signal numérique (DSP) programmé en assembleur. voir : - http://fr.wikipedia.org/wiki/Processeur_de_signal_num%C3%A9rique - http://www.orfony.fr/bdtech/DSP.html - ADSP-TS001 (Analog Device) - Stratix FPGA (Altera) Toutefois cette implémentation sur un simple ATmega à 4 euros n'a pas la prétention d’afficher des performances époustouflantes, mais elle permet de COMPRENDRE et de maîtriser la transformée de Fourier et de la voir fonctionner. ***********************************************************************/ void acquisition() { uint16_t acqH; uint16_t tab_acq[64]; uint8_t n, r, n_max; float Te; // période d'échantillonage float x; Te = 1.0 / frq_echantillonnage; uint16_t valeur_lue; if (bourrage) {n_max = nb_ech /4; } else {n_max = nb_ech; } //n_max = 16; for(n=0; n < n_max-1; n++) { ADCSRA |= _BV(ADSC); //Start conversion - resolution 10bits while (ADCSRA & _BV(ADSC) ) {;} // attend la fin de la converstion tab_acq[n] = ADCL; acqH = ADCH; // passage à 16 bits pour pouvoir décaller tab_acq[n] += acqH << 8; } for(n=0; n < n_max-1; n++) { valeur_lue =tab_acq[n]; if (hamming) { x = x * (1- cos (2* M_PI * n / n_max ));} x= (valeur_lue - 512.0) / 100.0; r=bit_reversal(n,nb_etapes); tab_X[r][1] = x; // partie reelle tab_X[r][2] = 0; // partie imaginaire } } void remplir_tableau_echantillons() { // création du signal à analyser uint8_t n, r, n_max; float Te; // période d'échantillonage float x; Te = 1.0 / frq_echantillonnage; if (bourrage==true) {n_max = nb_ech /4; } else {n_max = nb_ech; } for(n=0; n < n_max-1; n++) // nb d'échantillons { x= cos(2.0 * M_PI * frequence1 * n * Te ); if (hamming) { x = x * (1- cos (2* M_PI * n / n_max ));} r=bit_reversal(n,nb_etapes); tab_X[r][1] = x; // partie reelle tab_X[r][2] = 0; // partie imaginaire } } void calcul_tableau_W() { // calcul et memorisation dans un tableau des twiddle factors uint8_t n; float x; for(n=0; n<(nb_ech/2-1); n++) { x=2.0*M_PI * n / nb_ech; tab_W[n][1] = cos(x); // partie reelle tab_W[n][2] = -sin(x); // partie imaginaire } } void calcul_fourier() { complexe produit; // voir le type "complexe" déclaré plus haut uint8_t decal =2; uint8_t etape, e1, e2, li, w, ci; uint8_t li_max=nb_ech; e2=1; for (etape=1; etape<=nb_etapes; etape++) { e1=e2; //(e1 evite d'effectuer des divisions e2/2 plus bas) e2=e2+e2; for (li=0; li<li_max; li+=1) { ci=li & (e2-1); // ET bit à bit if (ci>(e1-1)) { w=li_max/e2*(li & (e1 -1)); // ET bit à bit calcul du numéro du facteur de tripatouillages W produit[1]=tab_W[w][1]*tab_X[li][1]-tab_W[w][2]*tab_X[li][2]; produit[2]=tab_W[w][1]*tab_X[li][2]+tab_W[w][2]*tab_X[li][1]; tab_X[li][1]=tab_X[li-e1][1]-produit[1]; tab_X[li][2]=tab_X[li-e1][2]-produit[2]; tab_X[li-e1][1]=tab_X[li-e1][1]+produit[1]; tab_X[li-e1][2]=tab_X[li-e1][2]+produit[2]; } } } } void tracer_signal() { float a, S; uint8_t r, memo_x, memo_y, n, x, y; x=0; y=24; for(n=0; n<32; n++) { memo_x = x; memo_y = y; x = 2*n; r=bit_reversal(n, nb_etapes); if (hamming ==0) {a = 10.0;} else {a=5.0;} S = 20.0 - a * tab_X[r][1]; // partie réelle if ( (abs(S) )< 48 ) {y= lrint(S);} else {y=1;} /** choisir une des trois lignes ci-dessous **/ //buffer_drawPixel(x, y); //buffer_trace_baton_V(x, y); buffer_trace_segment( memo_x, memo_y, x, y); } affi_buffer(84); } void tracer_tableau_valeurs() { uint8_t offset_y = 0; uint8_t n ; uint8_t memo_x, memo_y, x, y; float A; uint8_t z; if (bourrage) {z=15;} else {z=1;} x=0; y=offset_y; for(n=0; n<32; n++) { memo_x = x; memo_y = y; x = 2*n; //x = n; A = z *( tab_X[n][1] * tab_X[n][1] + tab_X[n][2] * tab_X[n][2]); A = sqrt(A); if ( (abs(A) )< 48 ) {y= lrint(A);} else {y=1;} /** choisir une des trois lignes ci-dessous **/ // buffer_drawPixel(x, 47-y); // la plus rapide, mais peu visible... // buffer_trace_baton_V(x, 1 + y); buffer_trace_segment( memo_x, memo_y, x, y); } affi_buffer(84); } void test_out(uint8_t etat) { if (etat == 1) { PORTD |= 0b00000010;} else {PORTD &= 0b11111101;} } int main(void) { init_ports(); InitADC(); // InitINTs(); _delay_ms(100); // define the 5 LCD Data pins: SCE, RST, DC, DATA, CLK lcd_init(&PORTB, PB1, &PORTB, PB0, &PORTB, PB2, &PORTB, PB3, &PORTB, PB4); // frequence1 = 100.0; // Hz frq_echantillonnage=3200.0; // Hz lcd_goto_LC(0,1); lcd_puts2("FTT ATmega32"); _delay_ms(1000); lcd_clear(); calcul_tableau_W(); for(;;) { //frequence1 = 310.0; // Hz for(uint8_t n=1; n<23; n++) { mode_affi = (PINA & 0b00000001) == 0; hamming = (PINA & 0b00000010) != 0; bourrage = (PINA & 0b00000100) != 0; //frequence1 += 30; RAZ_tableau_echantillons(); acquisition(); // remplir_tableau_echantillons(); if (mode_affi) { buffer_RAZ(); tracer_signal(); // entrée ATTENTION : il faut faire cet affichage AVANT de calculer la TF parce que les résultats écrasent le tableau d'entrée // _delay_ms(1); } if (! mode_affi) { calcul_fourier(); // 100..120ms buffer_RAZ(); // 1.4ms test_out(1); tracer_tableau_valeurs(); // 250 ms test_out(0); } lcd_goto_LC(5,0); if (! mode_affi) {lcd_puts2(" FFT ");} else {lcd_puts2(" Signal");} // 7 ms } } }
|
|
|
|
14 -
|
26 juin 2014:
L'acquisition fonctionne : je mets en ligne cette vidéo montrant le traitement du signal en temps réel pour une plage de fréquences de 300Hz à 2kHz environ.
28 juin 2014:
J'ai un peu optimisé la fonction d'acquisition ce qui permet d'augmenter la gamme de fréquences à analyser : elle s'étend maintenant de 10 kHz à 90 kHz (elle était de 300HZ à 2kHz dans la version précédente !). Ce qui est moins ridicule n'est-ce pas ? On est maintenant bien au delà du simple domaine audio.
|
J'ai supprimé une vidéo ici parce que Dailymotion m'y incrustait une pub au début. Ce site n'est pas un panneau publicitaire !
|
|
|
15 Remarques à propos de la vitesse :
|
La fréquence max est actuellement égale à 90 kHz.
- si l'on veut augmenter la vitesse d'acquisition et maîtriser précisément
sa durée d'exécution il y a lieu de remplacer la fonction "acquisition()" par
une routine écrite en assembleur et faire appel à une interruption pour le timing.
- si l'on veut de plus augmenter la vitesse du traitement de la FFT, il faudra
remplacer la fonction "calcul_fourier()" par une routine en assembleur, et en fait dans ce cas on envisagera de réécrire tout le programme en assembleur.
- si on désire une plus grande rapidité encore, on pourra se tourner vers
un microcontrôleur ARM cadencé à... 700 MHz (voire plus) et on pense alors bien sûr au Raspberry Pi !
- si l'on veut calculer encore plus vite on peut utiliser le processeur d'une carte graphique, ou au moins le FPU intégré dans les microprocesseurs de nos ordinateurs.
- et si... on exige encore plus de vitesse on se tournera vers un Field Programmable Gate Arrays (FPGA) ou processeur de signal numérique (DSP) programmé en assembleur.
voir :
- http://fr.wikipedia.org/wiki/Processeur_de_signal_num%C3%A9rique
- http://www.orfony.fr/bdtech/DSP.html
- ADSP-TS001 (Analog Device)
- Stratix FPGA (Altera)
Toutefois cette implémentation sur un simple ATmega à 4 euros n'a pas la prétention d’afficher des performances époustouflantes, mais elle permet de COMPRENDRE et de maîtriser la transformée de Fourier et de la voir fonctionner.
|
|
|
|
16 Version avec calculs en virgule fixe
J'ai modifié le code en effectuant les calculs de la FFT sur des nombres en virgule fixe (le processeur traite des entiers 16 bits ce qui lui va fort bien, au lieu de nombres à virgule flottante "float" ce qui est très lent).
Résultat : La FFT est calculée en 3,5ms au lieu de 120 ms !!!! Soit 34 fois plus vite ! Voici ce nouveau code. Mais maintenant ce qui reste très lent c'est l'affichage. Mais je vais résoudre ça Mille Millions de Mille Sabords !
CODE SOURCE pour ATmega32
/*************************** FFT.cpp par Silicium628 logiciel Libre Open Source ****************************/ #include <avr/io.h> #include <stdint.h> #include <stdlib.h> #include "timeout.h" // comprend : #define F_CPU 16000000UL // 16 MHz #include "LCD_5110-628.cpp" #include <math.h> const char *version = "4.2"; // ( signal entrant 10kHz à 90kHz ) //typedef float complexe[2]; typedef int16_t complexe_f[2]; // entier signé pour calculs (rapides) en virgule fixe //complexe tab_X[64]; // nb_ech valeurs traitées //complexe tab_W[32]; // nb_ech/2 complexe_f tab_X[64]; // nb_ech valeurs traitées complexe_f tab_W[32]; // nb_ech/2 float frequence1; // Hz float frq_echantillonnage; // Hz const uint8_t nb_etapes=6; uint8_t nb_ech = pow (2,nb_etapes); // nombre d'échantillons = 2 puissance(nb_etapes) char hamming; char bourrage; char mode_affi; void RAZ_tableau_echantillons() { uint8_t n; for(n=0; n < nb_ech; n++) { tab_X[n][1] = 0; // partie reelle tab_X[n][2] = 0; // partie imaginaire } } void init_ports (void) // ports perso // 0 = entree, 1=sortie ; les 1 sur les pins en entrees activent les R de Pull Up (tirage à VCC) { PORTA = 0b00000111; DDRA = 0b01111000; //PA7 en entree (ADC7 - entrée signal); PA0, PA1, PA2 jumpers à GND. PORTB = 0b00000000; DDRB |= 0b11111111; PORTC = 0b00000000; DDRC = 0b11111111; PORTD = 0b00000000; DDRD = 0b11111111; } /* The ADC module contains a prescaler, which generates an acceptable ADC clock fre- quency from any CPU frequency above 100 kHz. The prescaling is set by the ADPS bits in ADCSRA */ void InitADC (void) { // SFIOR = 0b10000000; // ADTS2,1,0 = 100 -> CAN declenché par Timer0 Overflow - p:218 ADMUX = 0b01000111; //Bit 7:6 = ADC Reference Selection = 01 -> AVCC ; //Bits 0:4 - Analog Channel Selection Bits et gain éventuel - p214 // ici Select pin ADC7 using MUX avec ref tension interne = AREF externe - pas de gain. /** CHOISIR UNE SEULE LIGNE CI-DESSOUS pour ADCSRA */ // parametrage gamme 8-90 kHz // ADCSRA = 0b10000010; // bit7: Activate ADC; ADPS2..0->Prescaler=f/4 ; bit5 = ADATE (ADC Auto Trigger Enable)->non utilisé ici - p:216 et 218 // parametrage gamme 4-56 kHz // ADCSRA = 0b10000011; // bit7: Activate ADC; ADPS2..0->Prescaler=f/8 ; bit5 = ADATE (ADC Auto Trigger Enable)->non utilisé ici - p:216 et 218 // parametrage gamme 2-31 kHz // ADCSRA = 0b10000100; // bit7: Activate ADC; ADPS2..0->Prescaler=f/16 ; bit5 = ADATE (ADC Auto Trigger Enable)->non utilisé ici - p:216 et 218 // parametrage gamme 1-15 kHz // ADCSRA = 0b10000101; // bit7: Activate ADC; ADPS2..0->Prescaler=f/32 ; bit5 = ADATE (ADC Auto Trigger Enable)->non utilisé ici - p:216 et 218 // parametrage gamme 300 Hz-8000 Hz // ADCSRA = 0b10000110; // bit7: Activate ADC; ADPS2..0->Prescaler=f/32 ; bit5 = ADATE (ADC Auto Trigger Enable)->non utilisé ici - p:216 et 218 // parametrage gamme 200 Hz- 4300 Hz ADCSRA = 0b10000111; // bit7: Activate ADC; ADPS2..0->Prescaler=f/32 ; bit5 = ADATE (ADC Auto Trigger Enable)->non utilisé ici - p:216 et 218 } uint8_t bit_reversal(uint8_t num, uint8_t nb_bits) { uint8_t r = 0, i, s; if ( num > 1<< nb_bits) { return 0; } for (i=0; i<nb_bits; i++) { s = (num & (1 << i)); if(s) { r |= (1 << ((nb_bits - 1) - i)); } } return r; } /*********************************************************************** Remarques : - si l'on veut augmenter la vitesse d'acquisition et maîtriser précisément sa durée d'exécution il y a lieu de remplacer la fonction "acquisition()" par une routine écrite en assembleur et faire appel à une interruption pour le timing. - si l'on veut de plus augmenter la vitesse du traitement de la FFT, il faudra remplacer la fonction "calcul_fourier()" par une routine en assembleur, et en fait dans ce cas on envisagera de réécrire tout le programme en assembleur. - si on désire une plus grande rapidité encore, on pourra se tourner vers un microcontrôleur ARM cadencé à... 700 MHz (voire plus) et on pense alors bien sûr au Raspberry Pi ! - si l'on veut calculer encore plus vite on peut utiliser le processeur d'une carte graphique, (par exemple en 2014 une Nvidia GeForce GTX680 dont le processeur tourne à à 2GHz- 2Go - DDR5 ou une Nvidia Quadro 6000 ) ou au moins le FPU intégré dans les microprocesseurs de nos ordinateurs. - et si... on exige encore plus de vitesse on se tournera vers un Field Programmable Gate Arrays (FPGA) ou processeur de signal numérique (DSP) programmé en assembleur. voir : - http://fr.wikipedia.org/wiki/Processeur_de_signal_num%C3%A9rique - http://www.orfony.fr/bdtech/DSP.html - ADSP-TS001 (Analog Device) - Stratix FPGA (Altera) Toutefois cette implémentation sur un simple ATmega à 4 euros n'a pas la prétention d’afficher des performances époustouflantes, mais elle permet de COMPRENDRE et de maîtriser la transformée de Fourier et de la voir fonctionner. ***********************************************************************/ void acquisition() { uint16_t acqH; uint16_t tab_acq[64]; uint8_t n, r, n_max; float x; uint16_t valeur_lue; if (bourrage) {n_max = nb_ech /4; } else {n_max = nb_ech; } //n_max = 16; for(n=0; n < n_max-1; n++) { ADCSRA |= _BV(ADSC); //Start conversion - resolution 10bits while (ADCSRA & _BV(ADSC) ) {;} // attend la fin de la converstion tab_acq[n] = ADCL; acqH = ADCH; // passage à 16 bits pour pouvoir décaller tab_acq[n] += acqH << 8; } for(n=0; n < n_max-1; n++) { valeur_lue =tab_acq[n]; x= (valeur_lue - 512.0) / 100.0; if (hamming) { x = x * (1- cos (2* M_PI * n / n_max ));} r=bit_reversal(n,nb_etapes); tab_X[r][1] = x * 16; // partie reelle - * 16 pour obtenir un nombre en virgule fixe tab_X[r][2] = 0; // partie imaginaire } } void remplir_tableau_echantillons() { // création du signal à analyser uint8_t n, r, n_max; float Te; // période d'échantillonage float x; Te = 1.0 / frq_echantillonnage; if (bourrage==true) {n_max = nb_ech /2; } else {n_max = nb_ech; } for(n=0; n < n_max-1; n++) // nb d'échantillons { x= cos(2.0 * M_PI * frequence1 * n * Te ); if (hamming) { x = x * (1- cos (2* M_PI * n / n_max ));} r=bit_reversal(n,nb_etapes); tab_X[r][1] = x; // partie reelle tab_X[r][2] = 0; // partie imaginaire } } void calcul_tableau_W() { // calcul et memorisation dans un tableau des twiddle factors uint8_t n; //float x; float x, cosx, sinx; for(n=0; n<(nb_ech/2-1); n++) { x=2.0*M_PI * n / nb_ech; cosx = 16 * cos(x); sinx = -16 * sin(x); tab_W[n][1] = round(cosx); // partie reelle tab_W[n][2] = round(sinx); // partie imaginaire } } void calcul_fourier() { complexe_f produit; // voir le type "complexe" déclaré plus haut uint8_t etape, e1, e2, li, w, ci; uint8_t li_max=nb_ech; e2=1; for (etape=1; etape<=nb_etapes; etape++) { e1=e2; //(e1 evite d'effectuer des divisions e2/2 plus bas) e2=e2+e2; for (li=0; li<li_max; li+=1) { ci=li & (e2-1); // ET bit à bit if (ci>(e1-1)) { w=li_max/e2*(li & (e1 -1)); // ET bit à bit calcul du numéro du facteur de tripatouillages W produit[1]=((tab_W[w][1]*tab_X[li][1]) - (tab_W[w][2]*tab_X[li][2])) >> 4; // le décallage ( /16) because multiplication en virgule fixe produit[2]=((tab_W[w][1]*tab_X[li][2]) + (tab_W[w][2]*tab_X[li][1])) >> 4; tab_X[li][1]=tab_X[li-e1][1]-produit[1]; tab_X[li][2]=tab_X[li-e1][2]-produit[2]; tab_X[li-e1][1]=tab_X[li-e1][1]+produit[1]; tab_X[li-e1][2]=tab_X[li-e1][2]+produit[2]; } } } } void tracer_signal() { int32_t a, S; uint8_t r, memo_x, memo_y, n, x, y; x=0; y=24; for(n=0; n<32; n++) { memo_x = x; memo_y = y; x = 2*n; r=bit_reversal(n, nb_etapes); if (hamming ==0) {a = 10;} else {a=5;} S = (a * tab_X[r][1]); // partie réelle S = S >> 4; S = 20 - S; if ( (abs(S) )< 48 ) {y= lrint(S);} else {y=1;} /** choisir une des trois lignes ci-dessous **/ //buffer_drawPixel(x, y); //buffer_trace_baton_V(x, y); buffer_trace_segment( memo_x, memo_y, x, y); } affi_buffer(84); } void tracer_tableau_valeurs() { uint8_t offset_y = 0; uint8_t n ; uint8_t memo_x, memo_y, x, y; uint32_t A; uint8_t z; if (bourrage) {z=15;} else {z=5;} x=0; y=offset_y; for(n=0; n<31; n++) // batons =3.5 ms ; segments = 86 ms { memo_x = x; memo_y = y; //x = n; x = 2*n; // largeur de la trace = 4 px (1 baton de 3px + 1 séparation de 1px) A = ((tab_X[n][1] * tab_X[n][1]) + (tab_X[n][2] * tab_X[n][2])); A >>=8; // div/256; // 256 = 16 * 16 (compense la multiplication en virgule fixe puis retour à une valeur ordinaire) A *= z; A = sqrt(A); if ( (abs(A) )< 48 ) {y= lrint(A);} else {y=47;} /** choisir une des trois lignes ci-dessous; ATTENTION : les rapidités ne sont pas les mêmes !! **/ // buffer_drawPixel(x, 47-y); // la plus rapide, mais peu visible... buffer_trace_baton_V(x, 1 + y); // buffer_trace_segment( memo_x, memo_y, x, y); } affi_buffer(84); // 12.6 ms } int main(void) { init_ports(); InitADC(); // InitINTs(); _delay_ms(100); lcd_init(); // frequence1 = 100.0; // Hz // frq_echantillonnage=3200.0; // Hz lcd_goto_LC(0,1); lcd_puts2("FTT ATmega32"); _delay_ms(1000); lcd_clear(); calcul_tableau_W(); lcd_goto_LC(5,0); if (! mode_affi) {lcd_puts2("TF Silicium628 ");} else {lcd_puts2(" Signal");} // 7 ms for(;;) { //frequence1 = 310.0; // Hz for(uint8_t n=1; n<23; n++) { mode_affi = (PINA & 0b00000001) == 0; hamming = (PINA & 0b00000010) != 0; bourrage = (PINA & 0b00000100) != 0; //frequence1 += 30; RAZ_tableau_echantillons(); acquisition(); // 7ms // remplir_tableau_echantillons(); if (mode_affi) { buffer_RAZ(); tracer_signal(); // entrée ATTENTION : il faut faire cet affichage AVANT de calculer la TF parce que les résultats écrasent le tableau d'entrée } if (! mode_affi) { calcul_fourier(); // 7 ms avec calculs en virgule fixe (int 16 bits) au lieu de 100..120ms avec calculs en virgule flotante (float 32 bits) buffer_RAZ(); // 1.4 ms tracer_tableau_valeurs(); // 16ms } } } }
|
|
|
|
17 Version turbo !
|
01 juillet 2014:
Après avoir diminué drastiquement la durée de calcul de la TF en utilisant un format de nombres en virgule fixe, je me suis attaqué à la partie affichage.
J'ai revu les fonctions de commande de l'afficheur LCD 5110, tout en gardant l'écriture en langage C.
Résultat : La boucle complète comprenant l'acquisition, le calcul FFT et l'affichage s’exécute en 28 ms à peine ! (Au départ on tournait à 400 ms environ).
Et ça change tout ! 28 ms ça permet de faire une analyse visuelle de l'audio en temps réel. Un "Analyser de spectre audio", vous savez avec des petites barres verticales qui dansent en mesure avec la musique. Et ça marche. Je vous posterai ici la vidéo prochainement.
On en voit partout de ces trucs là, dans les logiciels, sur Androïd etc...
Oui mais celui-ci on l'a fait entièrement nous même, en comprenant toutes les étapes du raisonnement qui conduit au résultat. Souvenez-vous, on est parti de ça ==>
|
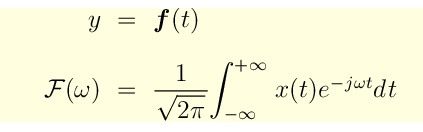 |
|
|
20 Le coin de l'ARDUINO
|
Moi qui apprécie bien les microcontrôleurs AVR je surveille du coin de l'oeil ce qui se passe au royaume de l'ARDUINO. On y rencontre visiblement pas mal de fous furieux dans mon genre. Mais l'aspect commercial de la chose m'a toujours rebuté. Toutefois avec l'apparition de nombreux clones les choses évoluent vers plus d'ouverture. Ce qui m'a vraiment intéressé ces temps derniers c'est la symbiose réussie entre des cartes puissantes (basées sur des ATmega 2560) et des petits afficheurs TFT couleur au format des téléphones portables (3.5") tactiles qui plus est.
J'ai donc décidé de tester ces bestioles et la transformée de Fourier était le projet idéal pour ça. Je me suis offert un clone SainSmart 2560 + Ecran TFT 320x240 px + carte d'adaptation servant à relier l'un à l'autre.
|
|
|
|
21 -
 |
 |
|
|
22 -
|
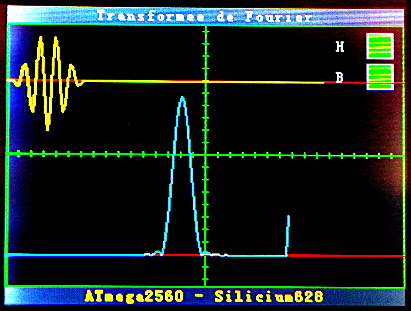
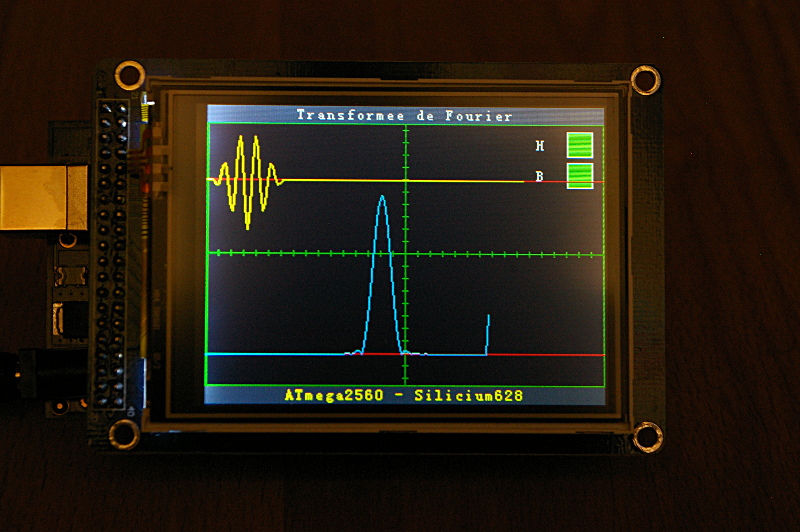
Après une demi journée pour apprivoiser l'animal (et réussir à le programmer en C++ avec Geany comme éditeur en remplacement de l'EDI Arduino qui ne me convenait pas) j'ai pu facilement adapter notre programme de Transformée de Fourier Rapide pour la carte Mega 2560 et l'afficheur TFT. Voici le résultat :
Les deux petits carrés verts à droite ce sont des boutons. si ! si ! lorsqu'on clique dessus avec un stylet, il s'allument et s’éteignent en modifiant au passage les paramètres du programme : celui du haut permet d'appliquer ou non la fenêtre de Hamming sur le signal d'entrée, et le second applique ou non le bourrage de zéros. Je vous montre cela en vidéo ci-dessous.
|
 |
|
|
23 -
|
|
Je tiens à préciser que la musique d'illustration de la vidéo ne constitue nullement le signal à analyser (Il est créé en interne par la fonction sinus...)
Mais bien entendu je vais activer la partie acquisition du signal d'entrée par le convertisseur ADC de l'ATmega. Comme d'habitude je vous tiens au courant de l'évolution des choses.
|
|
|
24 Le programme (firmware) en C++ pour la carte Mega2560 + TFT
CODE SOURCE pour ATmega2560
#include <UTFT.h> #include <ITDB02_Touch.h> #include <avr/io.h> #include <stdint.h> #include <stdlib.h> //#include "timeout.h" // comprend : #define F_CPU 16000000UL // 16 MHz #include <math.h> // Declare which fonts we will be using extern uint8_t SmallFont[]; // Arduino Mega: // ------------------- // Standard Arduino Mega/Due shield : <display model>,38,39,40,41 // CTE TFT LCD/SD Shield for Arduino Mega : <display model>,38,39,40,41 const char *version = "1.1"; // ( signal entrant 10kHz à 90kHz ) UTFT TFT320(ITDB32S,38,39,40,41); ITDB02_Touch TACTILE(6,5,4,3,2); typedef float complexe[2]; complexe tab_X[128]; // nb_ech valeurs traitées complexe tab_W[64]; // nb_ech/2 float frequence1; // Hz float frq_echantillonnage; // Hz const uint8_t nb_etapes=7; uint8_t nb_ech = pow (2,nb_etapes); // nombre d'échantillons = 2 puissance(nb_etapes) uint8_t hamming; uint8_t bourrage; uint8_t mode_affi; uint8_t etat_boutons; // 8 bits definissant chacun l'état d'un bouton, soit 8 boutons en tout void init_ports (void) // ports perso // 0 = entree, 1=sortie ; les 1 sur les pins en entrees activent les R de Pull Up (tirage à VCC) { PORTA = 0b00000111; DDRA = 0b01111000; //PA7 en entree (ADC7 - entrée signal); PA0, PA1, PA2 jumpers à GND. PORTB = 0b00000000; DDRB |= 0b11111111; PORTC = 0b00000000; DDRC = 0b11111111; PORTD = 0b00000000; DDRD = 0b11111111; } /* The ADC module contains a prescaler, which generates an acceptable ADC clock fre- quency from any CPU frequency above 100 kHz. The prescaling is set by the ADPS bits in ADCSRA */ void InitADC (void) { // SFIOR = 0b10000000; // ADTS2,1,0 = 100 -> CAN declenché par Timer0 Overflow - p:218 ADMUX = 0b01000111; //Bit 7:6 = ADC Reference Selection = 01 -> AVCC ; //Bits 0:4 - Analog Channel Selection Bits et gain éventuel - p214 // ici Select pin ADC7 using MUX avec ref tension interne = AREF externe - pas de gain. /** CHOISIR UNE SEULE LIGNE CI-DESSOUS pour ADCSRA */ // parametrage gamme 8-90 kHz // ADCSRA = 0b10000010; // bit7: Activate ADC; ADPS2..0->Prescaler=f/4 ; bit5 = ADATE (ADC Auto Trigger Enable)->non utilisé ici - p:216 et 218 // parametrage gamme 4-56 kHz // ADCSRA = 0b10000011; // bit7: Activate ADC; ADPS2..0->Prescaler=f/8 ; bit5 = ADATE (ADC Auto Trigger Enable)->non utilisé ici - p:216 et 218 // parametrage gamme 2-31 kHz // ADCSRA = 0b10000100; // bit7: Activate ADC; ADPS2..0->Prescaler=f/16 ; bit5 = ADATE (ADC Auto Trigger Enable)->non utilisé ici - p:216 et 218 // parametrage gamme 1-15 kHz // ADCSRA = 0b10000101; // bit7: Activate ADC; ADPS2..0->Prescaler=f/32 ; bit5 = ADATE (ADC Auto Trigger Enable)->non utilisé ici - p:216 et 218 // parametrage gamme 300 Hz-8000 Hz // ADCSRA = 0b10000110; // bit7: Activate ADC; ADPS2..0->Prescaler=f/32 ; bit5 = ADATE (ADC Auto Trigger Enable)->non utilisé ici - p:216 et 218 // parametrage gamme 200 Hz- 4300 Hz ADCSRA = 0b10000111; // bit7: Activate ADC; ADPS2..0->Prescaler=f/32 ; bit5 = ADATE (ADC Auto Trigger Enable)->non utilisé ici - p:216 et 218 } void RAZ_tableau_echantillons() { uint8_t n; for(n=0; n < nb_ech; n++) { tab_X[n][1] = 0; // partie reelle tab_X[n][2] = 0; // partie imaginaire } } uint8_t bit_reversal(uint8_t num, uint8_t nb_bits) { uint8_t r = 0, i, s; if ( num > 1<< nb_bits) { return 0; } for (i=0; i<nb_bits; i++) { s = (num & (1 << i)); if(s) { r |= (1 << ((nb_bits - 1) - i)); } } return r; } void acquisition() { uint16_t acqH; uint16_t tab_acq[64]; uint8_t n, r, n_max; float x; uint16_t valeur_lue; if (bourrage != 0) {n_max = nb_ech; } else {n_max = nb_ech /2; } //n_max = 16; for(n=0; n < n_max-1; n++) { ADCSRA |= _BV(ADSC); //Start conversion - resolution 10bits (0..1024) while (ADCSRA & _BV(ADSC) ) {;} // attend la fin de la converstion tab_acq[n] = ADCL; acqH = ADCH; // passage à 16 bits pour pouvoir décaller tab_acq[n] += acqH << 8; // ici tab_acq[n] = 0..1024 } for(n=0; n < n_max-1; n++) { valeur_lue =tab_acq[n]; x= (valeur_lue - 512.0) / 100.0; // 512 = 1024/2 if (hamming) { x = x * (1- cos (2* M_PI * n / n_max ));} r=bit_reversal(n,nb_etapes); tab_X[r][1] = x * 16; // partie reelle - * 16 pour obtenir un nombre en virgule fixe tab_X[r][2] = 0; // partie imaginaire } } void remplir_tableau_echantillons() { // création du signal à analyser uint8_t n, r, n_max; float Te; // période d'échantillonage float y; float a; Te = 1.0 / frq_echantillonnage; if (bourrage != 0) { n_max = nb_ech /4; } else { n_max = nb_ech; } for(n=0; n < n_max-1; n++) // nb d'échantillons { y= cos( 2.0 * M_PI * frequence1 * n * Te ); if (hamming) { y = y * (1- cos (2* M_PI * n / n_max ));} r=bit_reversal(n,nb_etapes); y *= 2; tab_X[r][1] = y; // partie reelle tab_X[r][2] = 0; // partie imaginaire } } void calcul_tableau_W() { // calcul et memorisation dans un tableau des twiddle factors uint8_t n; //float x; float x, cosx, sinx; for(n=0; n<(nb_ech/2-1); n++) { x=2.0*M_PI * n / nb_ech; tab_W[n][1] = cos(x); // partie reelle tab_W[n][2] = -sin(x); // partie imaginaire } } void calcul_fourier() { complexe produit; // voir le type "complexe" déclaré plus haut uint8_t etape, e1, e2, li, w, ci; uint8_t li_max=nb_ech; e2=1; for (etape=1; etape<=nb_etapes; etape++) { e1=e2; //(e1 evite d'effectuer des divisions e2/2 plus bas) e2=e2+e2; for (li=0; li<li_max; li+=1) { ci=li & (e2-1); // ET bit à bit if (ci>(e1-1)) { w=li_max/e2*(li & (e1 -1)); // ET bit à bit calcul du numéro du facteur de tripatouillages W produit[1]=(tab_W[w][1]*tab_X[li][1]) - (tab_W[w][2]*tab_X[li][2]); produit[2]=(tab_W[w][1]*tab_X[li][2]) + (tab_W[w][2]*tab_X[li][1]); tab_X[li][1]=tab_X[li-e1][1]-produit[1]; tab_X[li][2]=tab_X[li-e1][2]-produit[2]; tab_X[li-e1][1]=tab_X[li-e1][1]+produit[1]; tab_X[li-e1][2]=tab_X[li-e1][2]+produit[2]; } } } } void tracer_signal() { uint8_t offset_y = 60; int32_t a, S; uint8_t r, memo_x, memo_y, n, x, y; x=0; y= offset_y; TFT320.setColor(200, 0, 0); TFT320.drawLine(1,offset_y,319,offset_y); TFT320.setColor(255, 255, 0); TFT320.setBackColor(100, 100, 100); for(n=0; n<128; n++) { memo_x = x; memo_y = y; x = 2*n; r=bit_reversal(n, nb_etapes); if (hamming !=0) {a = 10.0;} else {a=20.0;} S = a * tab_X[r][1]; // partie réelle if ( (abs(S) )< 240 ) {y= lrint(S);} else {y=1;} /** choisir une des lignes ci-dessous **/ //buffer_trace_baton_V(x, y); y= offset_y - y; TFT320.drawLine(memo_x, memo_y, x, y); } // affi_buffer(84); } void tracer_tableau_valeurs() { uint8_t offset_x = 100; uint8_t offset_y = 200; uint8_t n ; uint8_t memo_x, memo_y, x, y; float A; uint8_t z; if (bourrage != 0 ) {z=4;} else {z=1;} x=0; y= offset_y; TFT320.setColor(200, 0, 0); TFT320.drawLine(1,offset_y,319,offset_y); TFT320.setColor(0, 180, 200); TFT320.setBackColor(0, 0, 0); for(n=0; n<64; n++) { memo_x = x; memo_y = y; //x = n; x = offset_x + 2*n; A = ((tab_X[n][1] * tab_X[n][1]) + (tab_X[n][2] * tab_X[n][2])); A = z * sqrt(A); if ( (abs(A) )< 240 ) {y= lrint(A);} else {y=240;} y= offset_y - y; /** choisir une des trois lignes ci-dessous; ATTENTION : les rapidités ne sont pas les mêmes !! **/ // buffer_drawPixel(x, 47-y); // la plus rapide, mais peu visible... // buffer_trace_baton_V(x, 1 + y); // buffer_trace_segment( memo_x, memo_y, x, y); //TFT320.drawPixel(x, 200-y); TFT320.drawLine(memo_x, memo_y, x, y); } // affi_buffer(84); // 12.6 ms } void trace_entete() { TFT320.setColor(64, 64, 64); TFT320.fillRect(0, 0, 319, 13); // bandeau en haut TFT320.setColor(64, 64, 64); TFT320.fillRect(0, 226, 319, 239); // bandeau en bas TFT320.setColor(255, 255, 255); TFT320.setBackColor(64, 64, 64); TFT320.print("Transformee de Fourier", CENTER, 1); TFT320.setColor(255,255,0); TFT320.print("ATmega2560 - Silicium628", CENTER, 227); } void trace_reticule() { // cadre TFT320.setColor(0, 150, 0); TFT320.setBackColor(0, 0, 0); TFT320.drawRect(0, 14, 319, 225); //reticule TFT320.drawLine(159, 15, 159, 224); TFT320.drawLine(1, 119, 318, 119); for (int i=9; i<310; i+=10) { TFT320.drawLine(i, 117, i, 121); } for (int i=19; i<220; i+=10) { TFT320.drawLine(157, i, 161, i); } } void trace_bouton(uint8_t n, uint8_t etat) { uint16_t position_x = 290; uint8_t dy = 25 * n; if (etat != 0) { TFT320.setColor(0, 255, 0); } else { TFT320.setColor(0, 80, 0); } TFT320.fillRoundRect(position_x, 20+dy, position_x+20, 40+dy); TFT320.setColor(255, 255, 255); TFT320.drawRect(position_x, 20+dy, position_x+20, 40+dy); } void trace_ecran() { TFT320.setColor(0, 0, 0); TFT320.setBackColor(0, 0, 0); TFT320.fillRect(0, 14, 319, 225); trace_entete(); trace_reticule(); trace_bouton(0, hamming); trace_bouton(1, bourrage); TFT320.setColor(255, 255, 255); TFT320.print("H", 265, 25); TFT320.print("B", 265, 50); } void setup() { randomSeed(analogRead(0)); InitADC(); TFT320.InitLCD(); TFT320.setFont(SmallFont); TFT320.clrScr(); TACTILE.InitTouch(LANDSCAPE); TACTILE.setPrecision(PREC_MEDIUM); trace_ecran(); } void polling_boutons() { uint8_t xt0 = 8; // position horizontale des boutons (alignés verticalement) uint8_t yt0; uint8_t ds = 8; // espacement vertical des boutons uint8_t xt, yt; while (TACTILE. dataAvailable() == true) { TACTILE.read(); xt = TACTILE.getX(); yt = TACTILE.getY(); TFT320.printNumI(xt, 280, 215, 3, ' '); TFT320.printNumI(yt, 280, 225, 3, ' '); yt0 = 28; // position verticale (centre) du premier bouton if ((xt > xt0-ds) && (xt < xt0+ds) && (yt > yt0-ds) && (yt < yt0+ds)) { etat_boutons ^=0b00000001; hamming = etat_boutons & 0b00000001; trace_ecran(); delay(300); } yt0 = 54; // position verticale (centre) du second bouton if ((xt > xt0-ds) && (xt < xt0+ds) && (yt > yt0-ds) && (yt < yt0+ds)) { etat_boutons ^=0b00000010; bourrage = etat_boutons & 0b00000010; trace_ecran(); delay(300); } } delay(100); } void loop() { randomSeed(analogRead(0)); frequence1 = 500.0; // Hz frq_echantillonnage=3200.0; // Hz calcul_tableau_W(); //frequence1 = 310.0; // Hz // for(uint8_t n=1; n<23; n++) // { //frequence1 += 30; RAZ_tableau_echantillons(); // acquisition(); // 7ms remplir_tableau_echantillons(); tracer_signal(); // entrée ATTENTION : il faut faire cet affichage AVANT de calculer la TF parce que les résultats écrasent le tableau d'entrée calcul_fourier(); // 7 ms avec calculs en virgule fixe (int 16 bits) au lieu de 100..120ms avec calculs en virgule flotante (float 32 bits) tracer_tableau_valeurs(); // 16ms polling_boutons(); }
|
|
|
|
25 Documents pour l'ARDUINO (ou clone)
Cette archive comprend le fichier principal (.ino) et les bibliothèques incluses (UTFT à ne pas confondre avec FFT, TFT c'est pour l'afficheur TFT) et ITDB02_Touch.cpp pour la partie tactile de l'afficheur)
|
|
|
|
26 Une application sur ESP32 :
|
|
 |
|
|
|