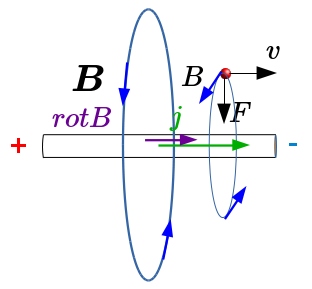
L'Electromagnétisme est une théorie relativiste
Dernière modif : 01/10/2016
L'Electromagnétisme est une théorie relativiste. D'ailleurs historiquement c'est l'étude de l'électricité et du magnétisme qui conduisit Einstein à la découverte de la relativité restreinte. Nous allons le démontrer mathématiquement.
[ lien vers L'article.pdf ]
articles précédent et suivant dans la série :
La Théorie de la relativité restreinte
VECTEURS


Ci-dessous le premier article de la série ANALYSE (complexe, harmonique):
Les nombres complexes


Ci-dessous le premier article de la série CALCUL VECTORIEL :
CALCUL VECTORIEL



Liens...

Ce que j'ai omis de dire dans cet article...

(volontairement pour ne pas trop alourdir l'article, ou par oubli... Mais je compte bien réparer ça ultérieurement: )
  • pourquoi la force dans le référentiel R' est-elle multipliée par 1/racine(v²/c²) ?
Remarque : J'ai rédigé cet article en Latex avec TexMacs sous Linux Min18 (TexMacs ne tourne pas sous Mint19 !!!)). Ensuite, afin de pouvoir l'afficher sur cette page html calculée en php, je l'ai exporté sous forme d'un document au format pdf.
4604
[ Retour Accueil ]
Ce site est développé en PHP avec des LOGICIELS LIBRES sous LINUX