Calcul des niveaux d'énergie dans l'atome d'hydrogène
par Silicium628
Rien de moins.
Nous calculerons au préalable l'altitude de l'orbite géostationnaire
puis nous démontrerons la seconde Loi de Kepler
pour nous faire la main.
RAPPEL DE CINÉMATIQUE |
Vitesse et accélération d'un point matériel dans un plan
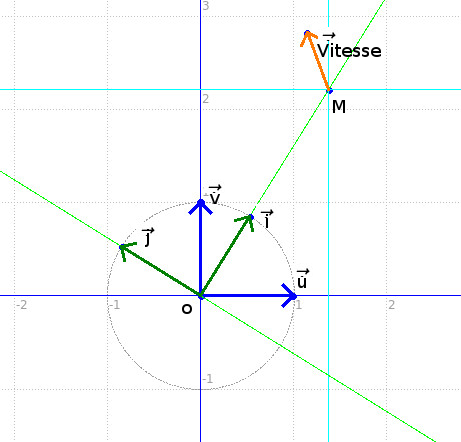 |
Soit
M un point matériel se déplaçant dans un plan muni d'un de repère
orthonormé Associons au point M le vecteur OM de module  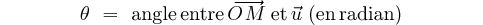 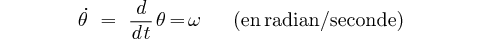 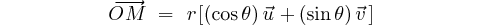 Remarque: On notera les dérivées avec un point au dessus, ex: 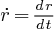
|
Relations entre les deux systèmes de coordonnées:
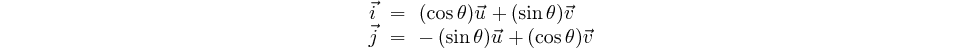
Nous en déduisons que:
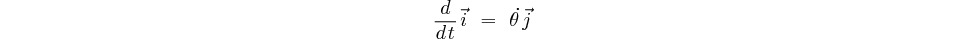
démonstration:
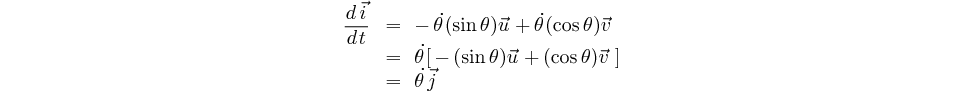 |
Nous en déduisons également:
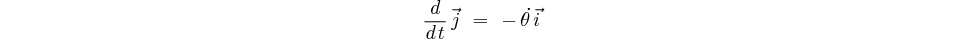
démonstration:
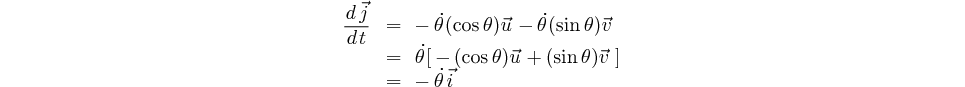 |
Calculons l'expression de la vitesse:
Calcul du vecteur vitesse:
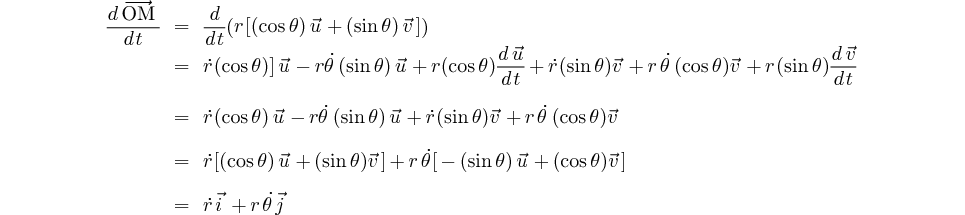
Calcul du vecteur vitesse directement dans le repère tournant:
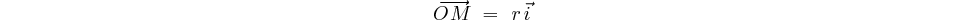
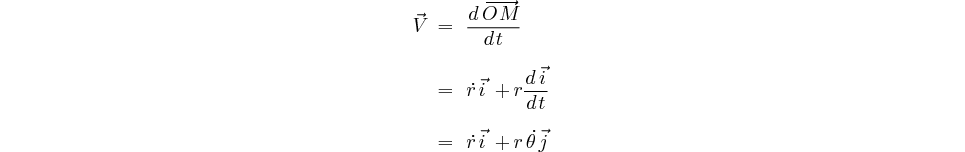
Calcul de l'accélération
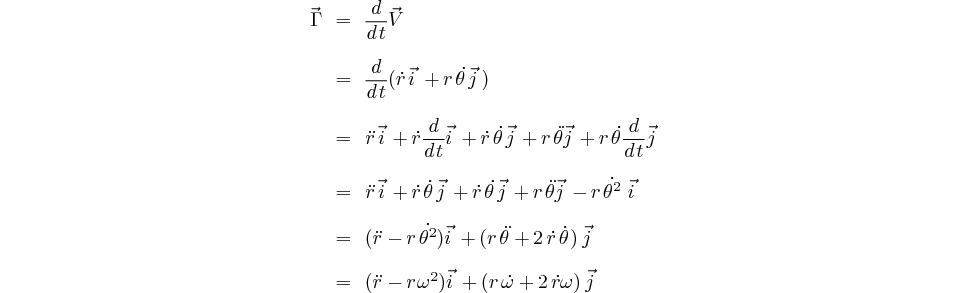
Cas où 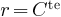 et
et 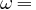 Cte
Cte
Dans le cas où le rayon vecteur est de longueur constante (le point matériel suit une trajectoire circulaire) et la vitesse de rotation est constante, nous avons:
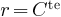 |
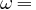 Cte Cte |
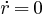 |
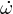 = 0 = 0 |
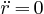 |
ce qui donne 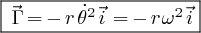
L'accélération est alors radiale (la composante tangentielle
suivant 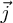 est nulle) et son module
est de valeur bien connue
est nulle) et son module
est de valeur bien connue 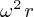 le signe
(-) indiquant qu'elle est dirigée en sens contraire de
le signe
(-) indiquant qu'elle est dirigée en sens contraire de 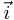 , c'est à dire vers l'intérieur de la
trajectoire (vers le centre du cercle), elle est dite centripète.
, c'est à dire vers l'intérieur de la
trajectoire (vers le centre du cercle), elle est dite centripète.
C'est à peu de chose près ce qui se passe pour les satellites
géostationnaires.
APPLICATIONS
I - Calcul de l'altitude de l'orbite géostationnaire: |
Un
satellite géostationnaire de masse 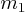 décrivant une orbite circulaire de rayon
décrivant une orbite circulaire de rayon 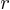 est attiré par la Terre de masse
est attiré par la Terre de masse 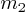 avec une force
avec une force 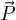 (son
poids)
(son
poids)
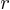 n'étant pas
la hauteur du satellite au dessus du sol (l'altitude) mais sa distance
par rapport au centre de la Terre.
n'étant pas
la hauteur du satellite au dessus du sol (l'altitude) mais sa distance
par rapport au centre de la Terre.
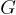 est la
constante de gravitation universelle
est la
constante de gravitation universelle
Cette force dirigée vers le centre incurve sa
trajectoire, qui sans cela serait une ligne droite. Si bien que son
mouvement est accéléré suivant le vecteur 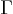 dont on vient de calculer l'expression.
dont on vient de calculer l'expression.
La loi fondamentale de la dynamique (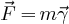 ) nous donne:
) nous donne:
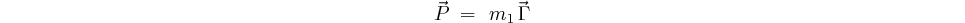
De ces deux équations nous déduisons:
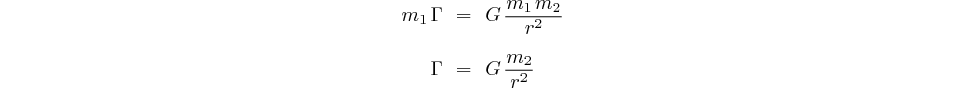
Nous voyons déjà que la masse 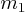 du satellite n'intervient pas dans le
calcul
du satellite n'intervient pas dans le
calcul
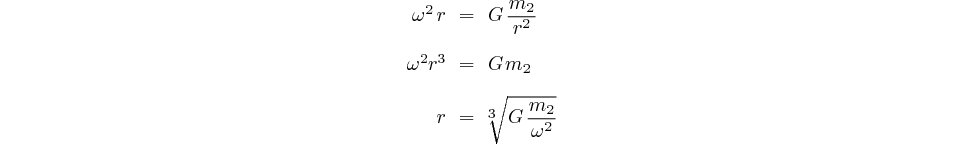
Remarque: 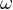 est connu puisque le satellite restant toujours à la verticale d'un
même point de l'équateur fait un tour par 23h56'. (24h00 par rapport au
Soleil, mais 23h56 par rapport aux étoiles dites « fixes » durée du
jour sidéral soit 86164s)
est connu puisque le satellite restant toujours à la verticale d'un
même point de l'équateur fait un tour par 23h56'. (24h00 par rapport au
Soleil, mais 23h56 par rapport aux étoiles dites « fixes » durée du
jour sidéral soit 86164s)
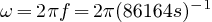 de dimension
de dimension
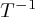
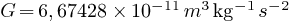 de dimension
de dimension
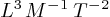
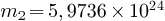 kg de
dimension
kg de
dimension 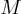
Vérifions l'homogénéité de la formule avant de nous lancer dans le calcul numérique:
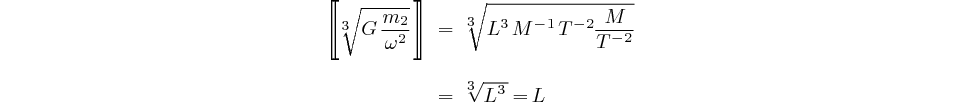
et 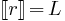 (également),
la formule est homogène du point de vue de équations aux dimensions. On
peut donc utiliser la calculatrice:
(également),
la formule est homogène du point de vue de équations aux dimensions. On
peut donc utiliser la calculatrice:
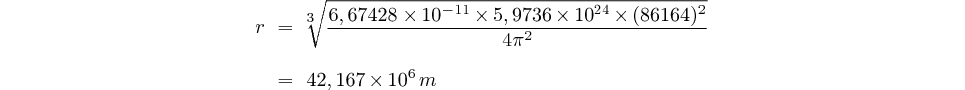
Soit 42 167 km du centre de la Terre.
Soustrayons les 6378 km du rayon équatorial pour obtenir l'altitude:
42167 - 6378 = 35789 km
Je lis ici et là 35784 km... je vous laisse
trouver où se cachent les 5 km d'écart...
II - Démonstration de la seconde loi de Kepler |
"Le
rayon vecteur qui lie une planète au soleil balaie des aires égales en
des temps égaux".
Kepler l'a constaté en analysant les données astronomiques recueillies grâce à l'observation par Tycho Brahe et en a déduit que le soleil exerce une force d'attraction centrale sur la planète.
En voici la démonstration inverse à partir des lois de la dynamique.
Considérons le cas d'un objet de masse 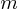 , une planète, une comète ou un
astéroïde par exemple, passant dans le champ d'attraction d'un objet de
masse
, une planète, une comète ou un
astéroïde par exemple, passant dans le champ d'attraction d'un objet de
masse 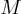 beaucoup plus importante que
beaucoup plus importante que
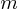 , une étoile par exemple.
Considérons
, une étoile par exemple.
Considérons 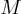 comme immobile et
plaçons la en O de notre graphique, liée au repère cartésien orthonormé
comme immobile et
plaçons la en O de notre graphique, liée au repère cartésien orthonormé
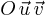 .
.
La masse 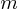 ,
quelle que soit sa vitesse au départ et la direction de sa trajectoire
est soumise à une force unique due à l'attraction gravitationnelle que
,
quelle que soit sa vitesse au départ et la direction de sa trajectoire
est soumise à une force unique due à l'attraction gravitationnelle que 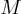 exerce sur elle. Les lois de la
physiques démontrables en laboratoire à notre échelle nous indiquent
que cette force est appliquée sur
exerce sur elle. Les lois de la
physiques démontrables en laboratoire à notre échelle nous indiquent
que cette force est appliquée sur 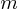 et est dirigée dans la direction de
et est dirigée dans la direction de 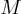 .
On dit qu'elle est « centrale ».
.
On dit qu'elle est « centrale ».
Elle a pour valeur:
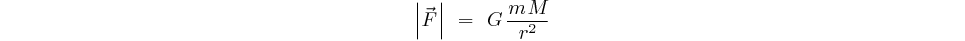
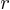 étant la
distance séparant les deux masses et
étant la
distance séparant les deux masses et 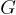 la constante de la Gravitation Universelle.
la constante de la Gravitation Universelle.
Si nous représentons cette force dans le repère
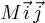 , nous voyons que le fait que la
force soit centrale implique que la composante suivant
, nous voyons que le fait que la
force soit centrale implique que la composante suivant 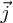 est nulle.
est nulle.
On peut donc écrire:
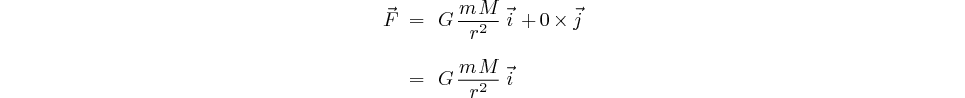
Cette force exercée sur la masse 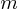 provoque son accélération
provoque son accélération
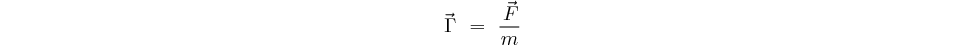
 étant un
scalaire, les vecteurs
étant un
scalaire, les vecteurs  et
et  sont colinéaires,
sont colinéaires, 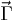 a tout comme
a tout comme 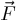 sa composante suivant
sa composante suivant 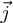 nulle.
nulle.
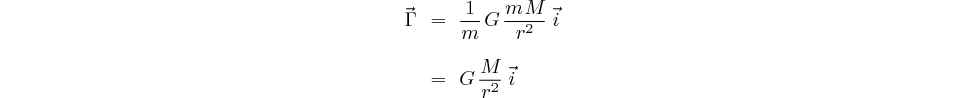
Notons au passage que 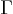 dépend
de
dépend
de 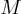 et de
et de 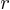 mais pas de
mais pas de 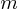 . C'est ce
qu'on nomme « l'accélération de la pesanteur »
. C'est ce
qu'on nomme « l'accélération de la pesanteur »
Nous avons d'autre part calculé plus haut la
valeur de 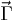 pour un point matériel
en déplacement:
pour un point matériel
en déplacement:
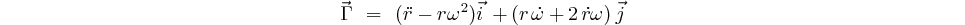
En égalant ces deux expressions nous obtenons:
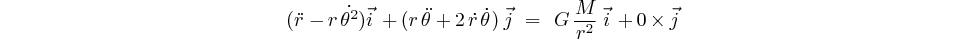
Il en résulte deux égalités distinctes, une
concernant la composante 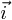 et
l'autre la composante
et
l'autre la composante 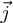
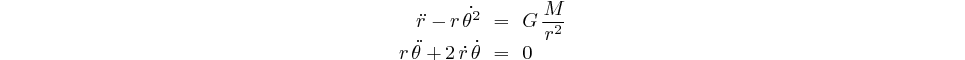
La première égalité nous a servi à calculer la taille de l'orbite d'un satellite en fonction de la masse centrale et de la période de révolution.
C'est maintenant à la deuxième égalité que nous allons nous intéresser:
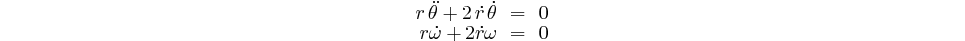
C'est une équation différentielle à variables séparables:
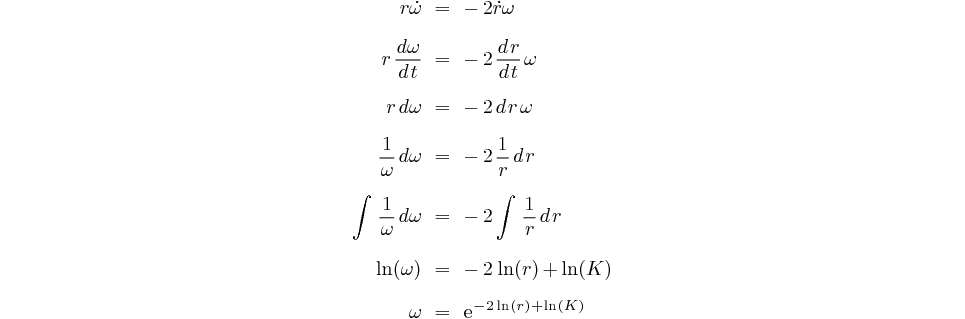
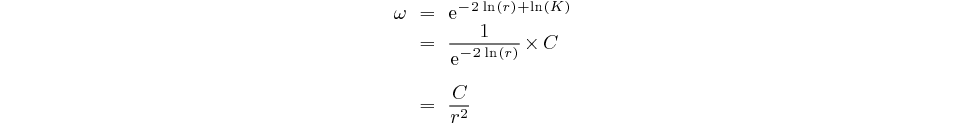
Donc 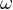 est
inversement proportionnel à
est
inversement proportionnel à 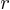 ² ,
voyons la conséquence que cela implique.
² ,
voyons la conséquence que cela implique.
Calculons l'aire balayée par le rayon vecteur
lorsque l'objet se déplace entre les points A et B de sa trajectoire:
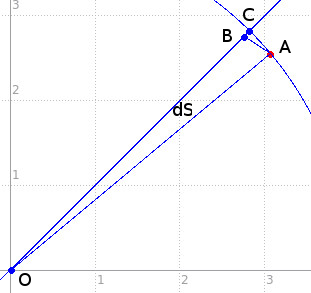 |
Si on considère un déplacement très petit, la longueur de la portion de trajectoire AB peut être confondue avec la longueur de l'arc AC centré sur le point d'attraction O.
Cette longueur a pour valeur:
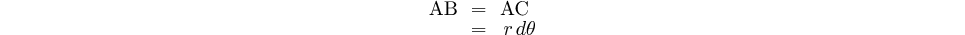
Les points B et C peuvent êtres confondus, la
surface 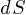 balayée vaut donc:
balayée vaut donc:
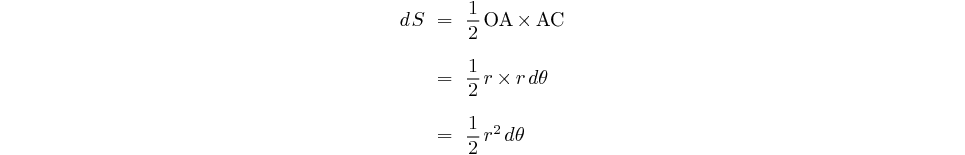
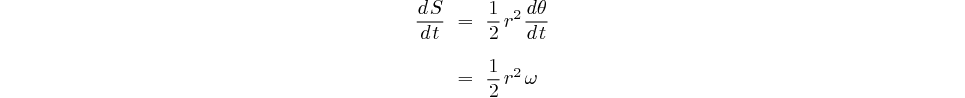
Et puisque nous avons trouvé que 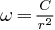 , il vient:
, il vient:
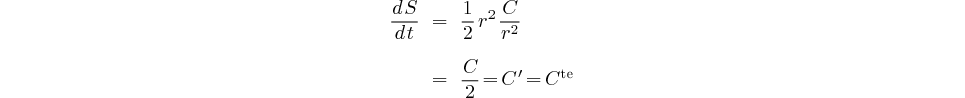
Intégrons pour trouver l'expression de l'aire en fonction du temps:
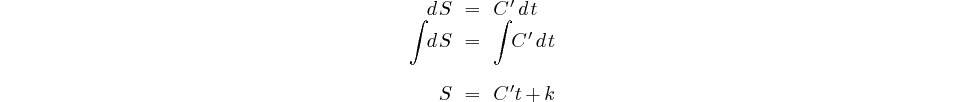
La surface balayée par le rayon vecteur est donc proportionnelle au temps.
Nous obtenons la seconde Loi de Kepler qui dit que les surfaces balayées en des temps égaux sont égales.
Nous sommes partis de la simple hypothèse que
la force est centrale pour arriver à cette conclusion. On pourrait donc
penser que c'est un effet de la force d'attraction. Mais que se
passerait-il si en O il n'y avait pas de masse attractive? On considère
par exemple un astéroïde qui passe par là, à des millions de km, mais
on « supprime le Terre » et, à la place, on dispose juste un petit
télescope... et bien la composante 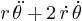 qui était nulle serait tout aussi nulle, et le calcul serait exactement
le même, la surface balayée par le rayon vecteur serait proportionnelle
au temps bien que l'astéroïde filerait tout droit. (Enfin, sur une
géodésique de l'espace-temps me dit Albert). Et il en serait de même de
n'importe quel corps se déplaçant en ligne droite observé de n'importe
que point de l'espace.
qui était nulle serait tout aussi nulle, et le calcul serait exactement
le même, la surface balayée par le rayon vecteur serait proportionnelle
au temps bien que l'astéroïde filerait tout droit. (Enfin, sur une
géodésique de l'espace-temps me dit Albert). Et il en serait de même de
n'importe quel corps se déplaçant en ligne droite observé de n'importe
que point de l'espace.
Donc la seconde Loi de Kepler est une
conséquence de l'absence d'effet de la masse centrale
sur l'axe ortho-radial .
III - Calcul des niveaux d'énergie et spectre de l'atome d'hydrogène |
Nous allons faire
le calcul sans utiliser
l'équation de Schrödinger (voir Bibliographie au bas de cette page). Le
calcul que nous allons faire tiendra
toutefois compte de la dualité onde-particule (thèse de Louis de
Broglie en 1924, qui lui valu le prix nobel en 1929) qui associe à
l'électron une onde de fréquence 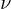 fonction de sa quantité de mouvement
tout en considérant encore l'électron
comme une particule ponctuelle soumise à une force centrale et en lui
appliquant les lois de la dynamique classique.
fonction de sa quantité de mouvement
tout en considérant encore l'électron
comme une particule ponctuelle soumise à une force centrale et en lui
appliquant les lois de la dynamique classique.
C'est donc une approche intermédiaire entre
l'électrodynamique classique et la mécanique quantique.
C'est l'approche de Bohr qui eu l'intuition que l'onde associée à
l'électron sur son orbite doit être stationnaire, c'est à dire que la
longueur de l'orbite doit être un multiple entier de sa longueur d'onde
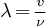 ,
, 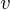 étant la vitesse de l'électron. Cette hypothèse restreint les orbites
possibles à certaines orbites stables, l'atome forme ainsi un système
quantifié. Les résultats du calculs sont conformes à l'expérience.
étant la vitesse de l'électron. Cette hypothèse restreint les orbites
possibles à certaines orbites stables, l'atome forme ainsi un système
quantifié. Les résultats du calculs sont conformes à l'expérience.
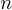 et pas des nombres
quantiques secondaires
et pas des nombres
quantiques secondaires 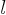 et
et 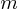 .
. Ce calcul est donc à à l'intersection de la mécanique classique, de la mécanique ondulatoire et de la mécanique quantique. Il en utilise d'ailleurs certains résultats, comme nous le verrons plus loin. Il n'en reste pas moins accessible à tous, ce qui n'est pas le cas d'un calcul efffectué totalement dans le formalisme de la mécanique quantique, avec l'équation de Schrödinger (voir la Bibliographie pour ceux qui veulent s'y lancer). Le résultat est précis (parce que nous connaissons les valeurs "qui marchent bien" des constantes physiques, certes).
Il ne faudra pas perdre de vue que compte tenu des résulats de la mécanique quantique, la position de l'électron dans l'atome ne peut pas être connue plus précisément qu'à 2 pi radians près... Ce qui signifie que cette position n'a pas de signification réelle.
Toutefois le côté résonnant de l'atome exposé ici est très parlant pour l'électronicien que je suis.
Pour aller plus loin, voir l'article l'Atome d'Hydrogène sur Wikipédia ainsi que les liens externes et la bibliographie au bas de cette page.
Hypothèses de base:
La description qui suit est celle d'un modèle (en l'occurrence le Modèle de Bohr).
Ce modèle est une représentation mentale de ce que semble être la réalité telle que nous la mesurons grossièrement avec nos instruments. Ce n'est pas LA réalité.
Ce modèle permet de calculer avec une certaine précision les raies spectrales de l'atome d'hydrogène, mais ne va guère au delà.
En particulier il échoue dans le cas d'atomes plus complexes. La mécanique quantique qui a ensuite été développée permet d'aller beaucoup plus loin, alors même
qu'elle est bien moins intuitive, ne permettant plus de se représenter une images simple de "la réalité", allant dans certaines de ses interprétations jusqu'à douter
qu'il existe une réalité bien définie avant que nous la mesurions ("réduction du paquet d'ondes").
Et c'est très bien ainsi, une pierre dans le jardin de ceux qui pensent que le futur est déjà écrit dans un Grand Livre !
Il semblerait en effet que la nature à cette échelle ne se laisse pas si facilement dessiner, mettre en images fussent-elles mentales...
Par exemple la représentation des particules accompagnée d'une "onde pilote" censée expliquer la "dualité onde-particule" (ou onde-corpuscule) suppose qu'il existerait bien une
particule ponctuelle ayant une position et une vitesse bien définie simultanément accompagnée par une onde. Et bien c'est une façon de se raccrocher à des préjugés qui
ne correspondent pas à ce que nous mesurons (remarque : ce que nous mesurons ne correspond pas non plus toujours à la réalité, lire les ouvrages d'Etienne Klein à ce sujet)
ni à ce que nous disent les équations de la mécanique quantique. On aurait pu s'en douter lorsqu'on affirmait qu'une particule "élémentaire"
possède une extension spatiale (taille) et un spin et qu'on suggère que le spin correspond à la rotation de cette entité de taille nulle. Il fallait oser !
Et comment un objet de taille nulle (ce qui devrait permettre de le situer dans l'espace avec une précision infinie) se révèle avoir des propriétés ondulatoires
(qui correspondent à un flou total quant à la position) ? Et les relations d'incertitudes de la mécanique quantique nous interdisent de connaitre
simultanémant la vitesse et la position de cette particule ponctuelle. Tout cela incite à penser que cette représentation d'une particule accompagnée de son onde pilote
est un concept très... flou ! Et bien "pire": le test des inégalités de Bell par les expériences d'Alain Aspect ("paradoxe EPR") confortent la
mécanique quantique dans ce qu'elle a de plus mystérieux : la non localité et l'intrication quantique.
L'abandon du concept de particule ponctuelle me semble inévitable. La position ne se concrétise que lors de la mesure, lors d'une interaction avec une autre entité donc.
Et avant la mesure il y avait quoi ? une onde ? oui sans doute. (remarque : l'expression "sans doute indique justement qu'il y a un doute !")
Un "champ quantique" ? Oui, ça c'est pas mal ! Plusieurs champs quantiques de natures différentes ? Oui c'est encore mieux, afin de rendre compte
de la pluralité des interactions connues. Et c'est quoi un champs quantique ? Ben c'est un truc qui se comporte comme un paquet d'onde qui peut se réduire en prenant
l'aspect (vu par nos instruments) d'une particule...
Faudrait quand même pas s'attendre à ce que les électrons soit faits de bois, les protons de silex et les neutrons de pâte à modeler ! Voire des micro-planètes avec des
plantes et des animaux dessus !!
Sur la page d'entrée de ce site vous trouverez des articles avec liens vers des vidéos de conférences portant sur la mécanique quantique et
les expériences d'Alain Aspect, ainsi que des conférences d'Etienne Klein.
A voir absolument.
Toutes ces précisions pour dire que la mécanique quantique est une théorie merveilleusement passionnante, je vous en parlerai d'une manière plus mathématique prochainement.
En attendant ces petits calculs sur le modèle de l'atome de Bohr permettent une approche approximative qui fonctionne... pas trop mal.
Voici donc les hypothèses simplissimes que nous retenons pour faire ces calculs :
L'atome d'hydrogène neutre est constitué d'un noyau (possédant un seul proton) autour duquel gravite un électron unique.
L'électron tourne autour du noyau de l'atome sur une orbite de rayon 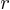 . Pour l'orbite fondamentale,
nous supposons le rayon de longueur constante (l'électron est considéré comme suivant une trajectoire circulaire) et la vitesse de rotation est supposée constante;
. Pour l'orbite fondamentale,
nous supposons le rayon de longueur constante (l'électron est considéré comme suivant une trajectoire circulaire) et la vitesse de rotation est supposée constante;
Nous avons:
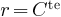 |
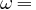 Cte Cte |
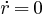 |
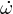 = 0 = 0 |
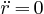 |
Nous supposons à priori que la vitesse de l'électron n'est pas relativiste, ce qui se vérifiera ensuite.
Début du calcul:
L'accélération ayant pour expression:
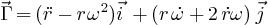
Elle se simplifie, compte tenu de l'hypothèse de départ pour devenir:
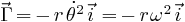
Cette accélération est donc radiale centrée sur la noyau (la
composante tangentielle suivant 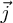 est nulle) et son module est de valeur
est nulle) et son module est de valeur 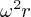 le signe (-) indiquant qu'elle est dirigée en sens contraire de
le signe (-) indiquant qu'elle est dirigée en sens contraire de 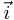 , c'est à dire vers l'intérieur de la
trajectoire (vers le centre du cercle), elle est dite centripète.
, c'est à dire vers l'intérieur de la
trajectoire (vers le centre du cercle), elle est dite centripète.
En valeur absolue cela donne:
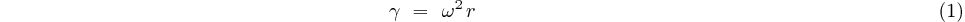
La vitesse de l'électron sur son orbite est:
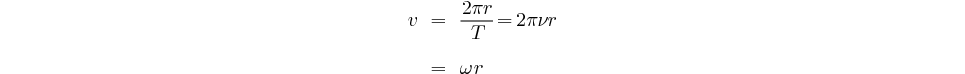
soit
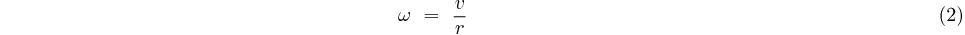
Remarque: en électronique
la fréquence est désignée par la lettre 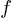 , en physique on
emploie le lettre grecque
, en physique on
emploie le lettre grecque 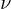 (nu)
(nu)
L'électron de charge électrique négative (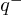 ) subit la force électrostatique (loi de Coulomb)
attractive de la part du noyau chargé positivement (
) subit la force électrostatique (loi de Coulomb)
attractive de la part du noyau chargé positivement (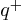 ), et que nous considèrerons comme
immobile étant donné qu'il est 1800 fois plus massif que l'électron.
), et que nous considèrerons comme
immobile étant donné qu'il est 1800 fois plus massif que l'électron.
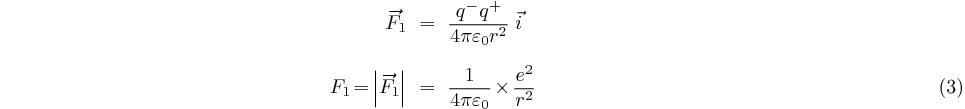
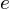 étant la charge de l'électron,
étant la charge de l'électron,
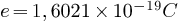
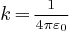 ,
, 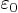 est la permittivité électrique du vide.
est la permittivité électrique du vide. 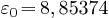
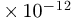 (SI)
(SI)
A cette échelle, la force d'attraction gravitationnelle, quant à elle, est négligeable devant cette force électrostatique.
L'énergie potentielle de l'électron soumis à cette force et à la
distance r du noyau est:
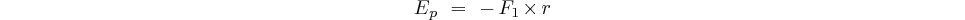
| Remarque:
Energie négative: Le signe (-) parce qu'il faut fournir de l'énergie à l'électron pour l'éloigner du noyau (et que l'énergie est nulle à l'infini, si on fournit l'énergie d'ionisation). Donc lorsque l'électron se trouve plus près du proton dans le champ coulombien, son énergie est inférieure à celle qu'il a lorsqu'il en est plus éloigné, inférieure donc à celle qu'il possède lorsqu'il en est infiniment éloigné, inférieure donc à zéro, c'est à dire négative. |
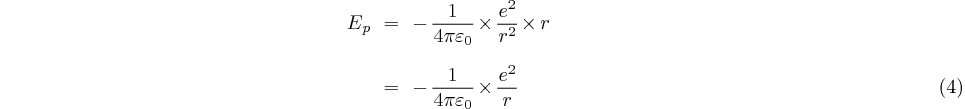
Nous avons vu plus haut que l'accélération centripète 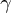 =
=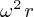 de
l'électron. Cette accélération est due à la force électrostatique
de
l'électron. Cette accélération est due à la force électrostatique 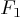 par l'intermédiaire de la relation qui
lie les forces et les accélérations de masses pesantes, à savoir la
relation fondamentale de la dynamique
par l'intermédiaire de la relation qui
lie les forces et les accélérations de masses pesantes, à savoir la
relation fondamentale de la dynamique
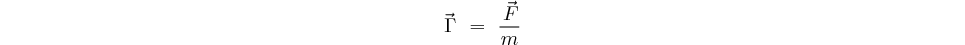
qui s'écrit ici
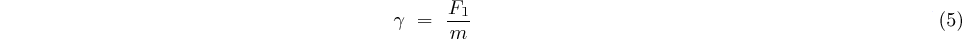
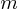 étant la masse de l'électron,
étant la masse de l'électron, 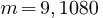
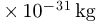
Vous ne m'entendrez pas souvent parler de « force centrifuge », si
force centrifuge il y a, c'est le noyau qui la subit. Si on supprime
instantanément le noyau d'un coup de baguette magique, l'électron
filera tout droit (avec une trajectoire ortho-radiale et non pas
radiale) et ce n'est certainement pas sous l'effet d'une quelconque «
force centrifuge », c'est juste le principe qui veut qu'un corps en
mouvement soumis à aucune force suit une trajectoire rectiligne à
vitesse constante.
En rapprochant les équations (1) et (4) nous obtenons la condition d'équilibre de l'orbite:
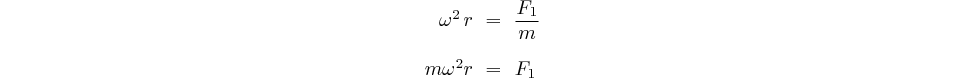
En remplaçant 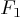 par sa valeur
trouvée en (3) il vient:
par sa valeur
trouvée en (3) il vient:
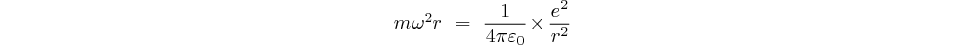
Remplaçons 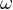 par sa valeur
par sa valeur 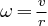 trouvée en (2):
trouvée en (2):
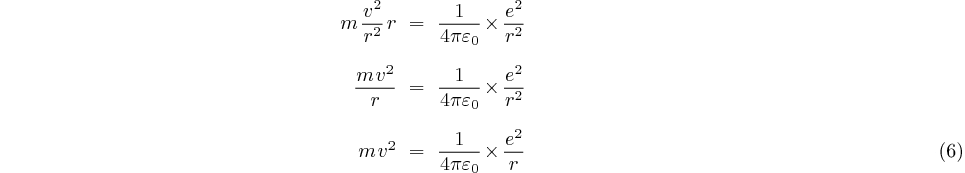
La vitesse 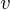 est donc telle que:
est donc telle que:
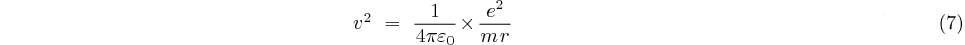
L'énergie potentielle calculée en (4) peut donc s'écrire:
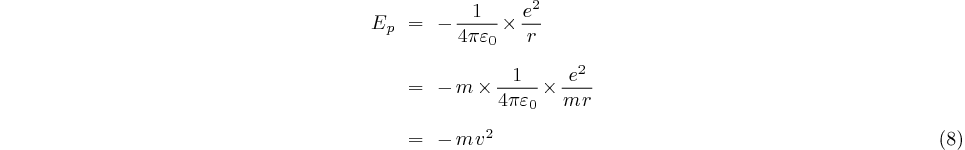
D'autre part l'énergie cinétique de l'électron de masse  a pour expression
a pour expression
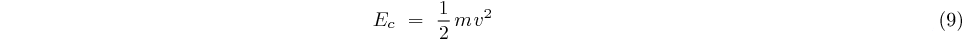
L'énergie totale de l'électron vaut donc:
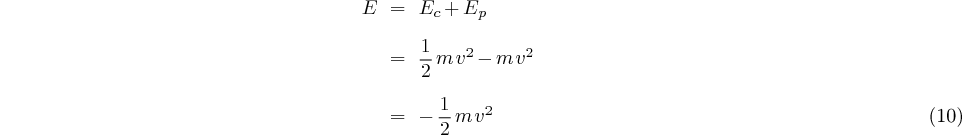
Nous avons vu dès le départ (hypothèse de Louis de Broglie) que
l'électron est associé à une onde (on peut dire qu'il se comporte comme
une particule ou une onde, c'est suivant... c'est un objet quantique!)
dont la longueur d'onde 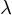 est
reliée à la quantité de mouvement de la particule par la relation:
est
reliée à la quantité de mouvement de la particule par la relation:
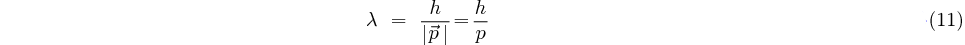
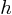 étant la constante de Planck
étant la constante de Planck
et la quantité de mouvement valant:
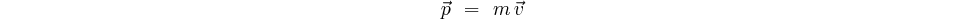

|
Remarque: Hypothèse de De Broglie pour une particule de masse non-nulle: 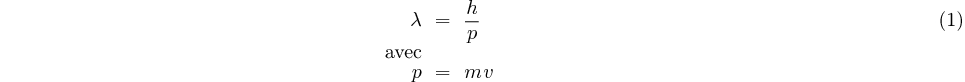
Prenons le cas du photon qui est une particule sans masse, mais qui possède un quanta d'énergie: 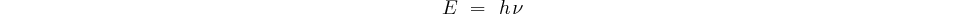 sa vitesse est ATTENTION: dans les lignes qui suivent je vais utiliser une notion de "masse équivalente à une énergie" Donc, d'après la relation d'équivalence entre masse et énergie (relation d'Einstein 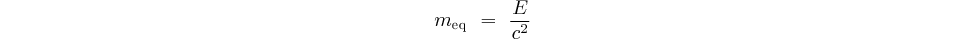
Cette « masse équivalente » ne conférerait-elle pas au photon
une « impulsion » ? Si cette « masse équivalente » était réelle, l'impulsion du photon (quantum d'impulsion) vaudrait: 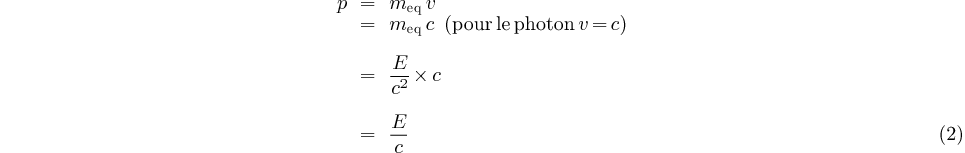 Il se trouve que c'est la bonne valeur. Reprenons maintenant l'hypothèse de de Broglie (1) et appliquons-la au photon compte tenu de ce dernier résultat (2): 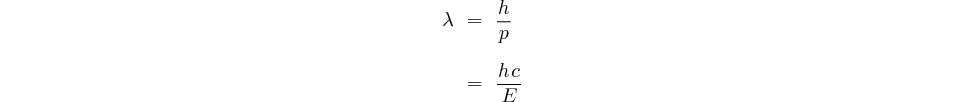
or il vient: 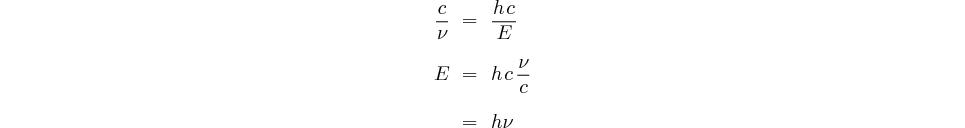
On retrouve ainsi la relation
de Planck-Einstein Refermons cette parenthèse en retenant seulement que la masse du photon EST NULLE. C'est la démonstration qu'on peut trouver des résultats exacts avec des hypothèses hasardeuses voire fausses! ( En fait de E=mc² il aurait fallu écrire E²= m²c⁴ + p²c² ) |
(11) et (12) donnent:
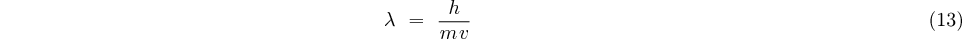
soit:
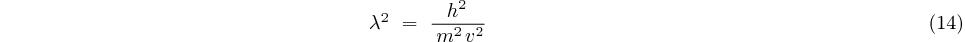
dans cette expression, remplaçons 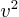 par sa valeur
par sa valeur 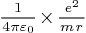 calculée en (7):
calculée en (7):
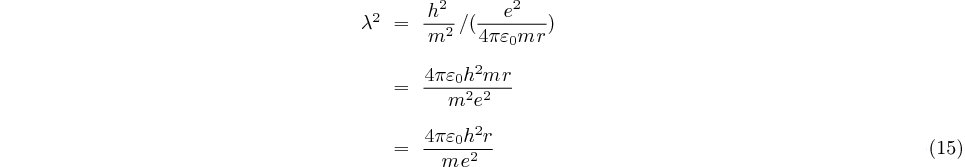
Nous allons maintenant poser une condition de résonance sur 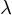 , ce qui va nous permettre de calculer
, ce qui va nous permettre de calculer 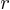 .
.
La longueur 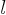 de l'orbite
(supposée circulaire) vaut:
de l'orbite
(supposée circulaire) vaut:

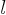 doit être un multiple de
doit être un multiple de 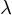 de façon à obtenir une onde
stationnaire:
de façon à obtenir une onde
stationnaire:

(16) et (17) puis donnent:
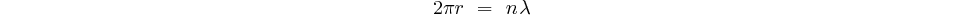
élevons au carré:
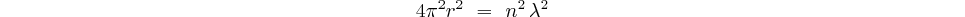
remplaçons 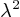 par sa valeur
trouvée en (15):
par sa valeur
trouvée en (15):
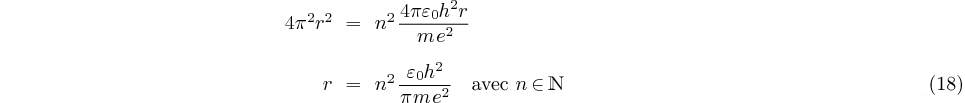
Le rayon 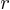 (et par conséquent la
vitesse, l'énergie, le rayonnement) ne peuvent prendre que des valeurs
discrètes, dites « quantifiées » en fonction de la valeur du nombre
entier
(et par conséquent la
vitesse, l'énergie, le rayonnement) ne peuvent prendre que des valeurs
discrètes, dites « quantifiées » en fonction de la valeur du nombre
entier 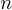 .
.
Ainsi 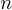 est un nombre
quantique pour l'atome. Ce n'est pas le seul, il y en a d'autres
qui définissent des modes de résonances plus complexes et se traduisent
par des dédoublements des raies spectrales. Nous ne considèrerons que
ce nombre quantique principal
est un nombre
quantique pour l'atome. Ce n'est pas le seul, il y en a d'autres
qui définissent des modes de résonances plus complexes et se traduisent
par des dédoublements des raies spectrales. Nous ne considèrerons que
ce nombre quantique principal 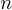 dans
cet article.
dans
cet article.
Pour n=1 l'atome se trouve dans son état d'énergie le plus bas
possible, on dit qu'il est dans son état
fondamental.
Les niveaux d'énergie de l'atome sont désignés par une lettre: K pour n=1, puis L, M,
N, etc...
Application numérique:
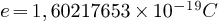
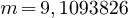
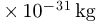
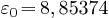
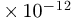
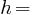 6,626068
6,626068 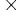 10-34
10-34
En faisant 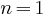 nous obtenons le
rayon de l'orbite la plus petite, dite première orbite de Bohr
correspondant à l'état fondamental de l'atome:
nous obtenons le
rayon de l'orbite la plus petite, dite première orbite de Bohr
correspondant à l'état fondamental de l'atome:
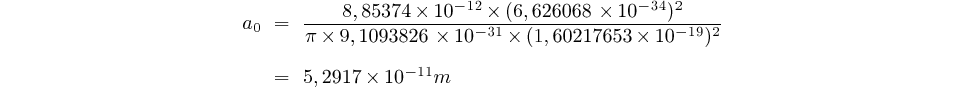
soit environ 53 picomètres (0,053 nm)
On peut écrire le rayon 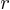 en
fonction de cette orbite de Bohr:
en
fonction de cette orbite de Bohr:
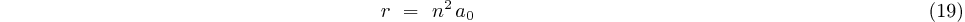
Calcul du spectre d'émission
Nous avons vu en (10) que l'énergie totale de l'électron est égale
à 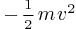
La vitesse (7) comme le rayon est aussi quantifiée:
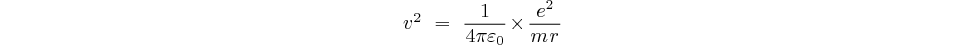
Remplaçons  par sa valeur
quantifiée trouvée en (18)
par sa valeur
quantifiée trouvée en (18)
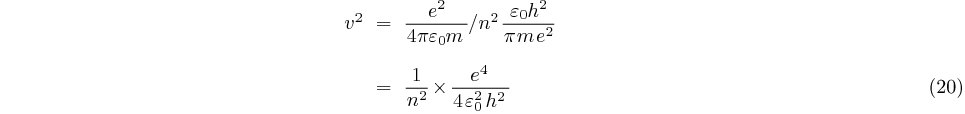
soit:
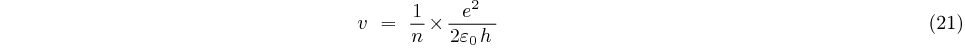
en posant 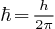 il vient: (
il vient: (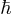 est la constante de Planck « réduite
»)
est la constante de Planck « réduite
»)
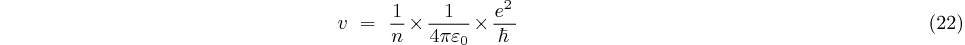
Cette vitesse de l'ordre de 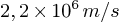 (pour n=1) est non
relativiste (0,7% c) mais elle est quand même étonnamment grande, 2000
km/s (seconde, pas heure!) sur un cercle aussi petit de moins de un
nanomètre! On peut donc s'attendre à une fréquence de révolution
énorme. Calculons-la par curiosité (bien que la mécanique quantique
nous indique que cela n'a pas vraiment de signification physique...)
(pour n=1) est non
relativiste (0,7% c) mais elle est quand même étonnamment grande, 2000
km/s (seconde, pas heure!) sur un cercle aussi petit de moins de un
nanomètre! On peut donc s'attendre à une fréquence de révolution
énorme. Calculons-la par curiosité (bien que la mécanique quantique
nous indique que cela n'a pas vraiment de signification physique...)
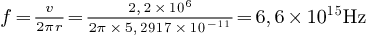
(attention, ce n'est pas la fréquence des photons émis lors de transitions de l'électron entre différentes orbites, quoi que du même ordre de grandeur que celle de photons UV, comme nous le verrons. Rappelons que tant que l'électron reste sur une orbite stable il ne rayonne pas).
Calcul de l'énergie:
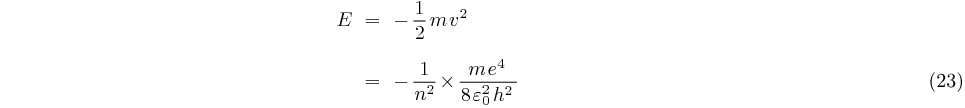
ou, en posant 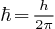
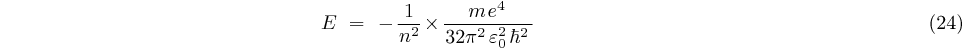
L'énergie maximale pour 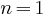 est
égale à l'énergie d'ionisation, elle vaut:
est
égale à l'énergie d'ionisation, elle vaut:
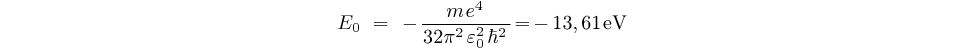
et l'énergie 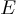 s'écrit alors:
s'écrit alors:
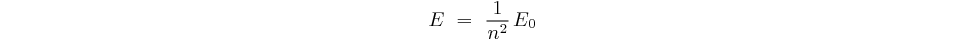
Rayonnement:
L'électron ne peut se trouver que sur une des
orbites permises correspondant à une valeur de 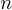 entière.
entière.
Un apport extérieur d'énergie (un photon incident) le fera "sauter" sur une orbite plus éloignée du noyau, et il « retombera » spontanément sur une orbite plus basse en émettant un photon d'énergie égale à la différence d'énergie entre celle qu'il avait sur l'orbite de départ et celle qui lui reste sur l'orbite d'arrivée.
Si donc on considère les valeurs 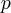 et
et 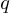 du nombre quantique
du nombre quantique 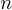 correspondant
à ces énergies de départ et d'arrivée,
correspondant
à ces énergies de départ et d'arrivée, 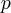 et
et 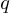 étant des nombres
entiers, on obtient des photons émis ayant comme énergie:
étant des nombres
entiers, on obtient des photons émis ayant comme énergie:
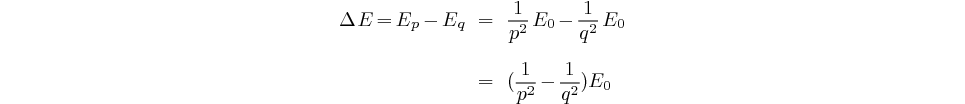
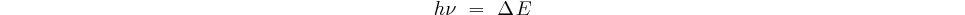
Les fréquences émises seront donc:
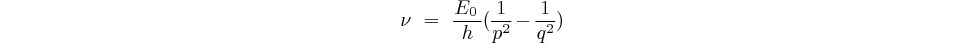
Et la longueur d'onde des photons émis sera:
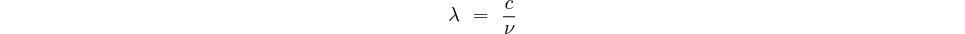
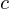 =
vitesse de la lumière dans le vide =
=
vitesse de la lumière dans le vide = 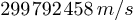
Calculons toutes ces valeurs avec un tableur (Le tableur libre
Open source de open office):
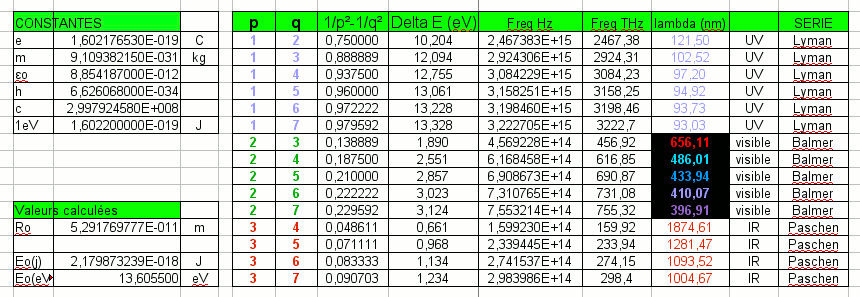 |
Toutes ce valeurs découlent du résultat Eo=13,6 eV.
Les valeurs données dans la littérature scientifique sont très très légèrement différentes)
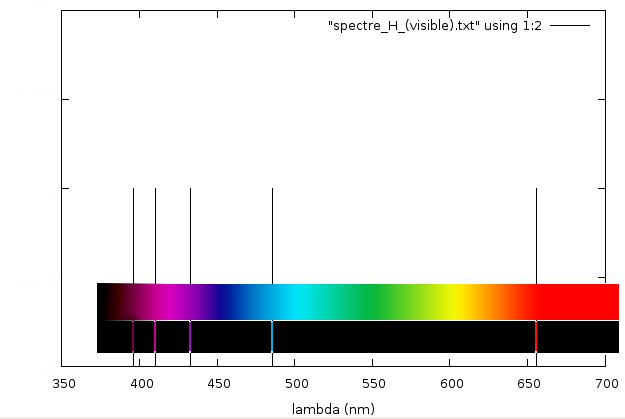
Les longueurs d'ondes comprises entre 400 et 700 nm se trouvent dans le domaine visible par l'Homme. Elles correspondent à des transitions entre les orbites 3, 4, 5, 6, 7 et l'orbite 2. Les raies spectrales correspondantes forment la série dite "de Balmer"
Voici la partie du spectre rayonné correspondant à cette série de Balmer (tracé automatiquement avec GNUplot):
Seules les trois raies les plus à droites sur ce graphique sont vraiment visibles. J'ai rajouté les couleurs approximativement...
La raie la plus lumineuse (rouge à 658,28 nm) qui correspond au saut entre le troisième et le second niveau d'énergie est appelée H alpha.
Elle est bien connue des astronomes qui utilisent des filtres adaptés pour augmenter le contraste des nébuleuses rayonnant principalement à cette longueur d'onde.
 |
Liens externes:
- http://fr.wikipedia.org/wiki/Spectre_de_l'atome_d'hydrogène
- http://fr.wikipedia.org/wiki/Atome_d'hydrogène
- http://fr.wikipedia.org/wiki/Orbitale_de_l'atome_d'hydrogène
- http://fr.wikipedia.org/wiki/Théorie_de_Schrodinger_de_l'atome_d'hydrogène
- http://fr.wikipedia.org/wiki/Hypothèse_de_De_Broglie
- http://fr.wikipedia.org/wiki/Série_de_balmer
- http://fr.wikipedia.org/wiki/H_alpha
Bibliographie:
- Le cours de Physique de FEYNMAN. mécanique quantique. Chapitre 19: l'Atome d'hydrogène. DUNOD (2000) - Dans lequel Feynman résout l'équation de Schrödinger.
- Le cours de Physique de FEYNMAN. mécanique quantique. Chapitre 2: La relation entre les points de vue ondulatoire et corpusculaire. Dans lequel Richard Feynman calcule la taille de l'atome d'hydrogène d'un manière surprenante (en trois lignes, par le calcul du minimum d'énergie en annulant sa dérivée)
- PHYSIQUE MP2/PC2 tome 2: caractère quantique - matière et
rayonnement. par C Janot et M. Gerl collection HACHETTE UNIVERSITE (1970) (grand
classique des universités)
- PHYSIQUE Terminale C.E
(1983) Auteurs: Alain Pénigaud, Lucien Quaranta, Jean Duboc. chez
FERNAND NATHAN
Silicium628
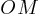 est appelé le « rayon
vecteur »
est appelé le « rayon
vecteur »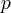 = impulsion
= impulsion 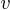 = vitesse de la particule
= vitesse de la particule 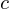 (vitesse de la lumière dans le vide)
(vitesse de la lumière dans le vide)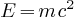 ),
l'énergie du photon est "équivalente" à une masse:
),
l'énergie du photon est "équivalente" à une masse: 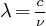
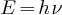 donnant la valeur de l'énergie du photon (quanta d'énergie) en fonction
de sa fréquence.
donnant la valeur de l'énergie du photon (quanta d'énergie) en fonction
de sa fréquence.